Category Archives: praca magisterska

prezentowana praca jest pracą magisterską

Zespół hamowania jazdy żurawia samojezdne­go

Weźmy pod uwagę zespół hamowania jazdy żurawia samojezdne­go. Składa się on z hydraulicznego układu hamowania 1 i ha­mulca ręcznego 2.  Przyjmijmy najpierw jako kryterium nie­sprawności zespołu hamowania fizyczny i umowny brak możliwości hamowania, przy czym niesprawność fizyczna oznacza brak możli­wości hamowania w ogóle, a niesprawność umowna to taka zmiana stanu technicznego zespołu, która nie przerywa wprawdzie funk­cjonowania tego zespołu, ale znacznie zwiększa ryzyko powsta­nia niesprawności fizycznej. Niesprawnością umowną zespołu ha­mowania jest więc na przykład niesprawność hamulca ręcznego, nawet przy prawidłowo działającym hydraulicznym układzie hamo­wania. Przy takiej definicji niesprawności zespołu hamowania ma on strukturę szeregową w sensie niezawodności (rys.4a). Je­żeli jednak przyjąć, że niesprawnością zespołu hamowania jest każde zdarzenie uniemożliwiające fizyczne jego funkcjonowanie, to zespołowi temu należy przypisać strukturę złożoną z elementu podstawowego (hydrauliczny układ hamowania) i z elementu stanowiącego rezerwę nieobciążoną (hamulec ręczny) (rys.4b).

  1. a) b)

r1

Rys. 2. Modele struktury niezawodnościowej zespołu hamowania [24]

Jak wynika z tych rozważań, możliwe są różne definicje opisowe niesprawności obiektu złożonego z wielu PK (więcej niż 1). Każdej z tych definicji może odpowiadać nie tylko in­na struktura niezawodnościowa, lecz również inne zbiory PK  i kryteriów ich niesprawności. Zatem ustalenie definicji nie­sprawności obiektu złożonego i wielu PK i dokładne określenie kryteriów niesprawności, precyzujących tę definicję, ma bar­dzo duże znaczenie w procesie tworzenia niezawodnościowego modelu tego obiektu.

Nie ma, niestety, ogólnie obowiązujących reguł, które po­zwalałyby do konkretnego obiektu dobierać odpowiednią defini­cję niesprawności. Wydaje się, że podstawą tego wyboru, a więc również wyboru struktury niezawodnościowej, może być na przykład ana­liza najważniejszych czynników mających wpływ na ten wybór:

  • rodzaju zadań przewidzianych do wykonania przy użyciu tego obiektu (lub maszyny zawierającej ten obiekt);
  • sposobu eksploatacji;
  • możliwości powstania dużych strat ekonomicznych i możli­wości zagrożenia dla życia ludzkiego w przypadku powstania niesprawności.

Wykażmy na przykładach wpływ każdego z nich na wybór kry­teriów niesprawności obiektu.

Najważniejszym kryterium oceny obiektów, przy użyciu któ­rych są wykonywane szczególnie odpowiedzialne zadania, jest skuteczność wykonania tych zadań. Znacznie mniej ważne są inne kryteria, np. koszty związane z funkcjonowaniem obiektu. Przy­kładem takiego obiektu może być żuraw samojezdny w warunkach wojny. Wówczas na skuteczność działania przy użyciu takiego obiektu ma duży wpływ zdolność nieulegania niesprawnością fi­zycznym. W takich przypadkach może być uzasadnione pomijanie w definicji niesprawności innych zdarzeń.

Duży wpływ na sformułowanie definicji niesprawności ma również sposób eksploatacji. W przypadku obiektów jednorazowe­go użytku lub obiektów funkcjonujących w sposób ciągły, tzn. bez planowanych przerw w pracy, pojęcie niesprawności umownych traci sens, bo nie ma okazji do ich usunięcia. Do takich obiek­tów nie mogą więc być dobierane takie definicje, jak na przy­kład podana powyżej definicja.

Szczególnie duży wpływ na wybór kryteriów niesprawności może mieć trzecia grupa czynników. Możliwość powstania dużych strat ekonomicznych i szczególnie dużych strat społecznych, jakimi są utrata życia lub zdrowia ludzkiego, związana jest z rodzajem zadania wykonywanego przy użyciu rozpatrywanego obiektu. W tych przypadkach ma sens wyróżnianie niesprawności umownych, bo ich usuwanie może zmniejszać ryzyko powstania tych strat.

W wyniku przedstawionego w tym podrozdziale postępowania, przebiegającego w wymienionych czterech etapach, powstaje no­minalny model niezawodnościowy obiektu. Na model ten składają się: opis procesu eksploatacji (lub zewnętrznych oddziaływań), opis zjawisk fizycznych przebiegających w poszczególnych PK, zbiór definicji i kryteriów niesprawności poszczególnych PK i całego obiektu, opis słowny lub graficzny (np. w postaci przedstawionej na rys.4) struktury niezawodnościowej.

W celu umożliwienia badań teoretycznych informacje zawar­te w modelu nominalnym w postaci opisu słownego i graficznego należy przedstawić za pomocą opisu matematycznego. Dokonuje się tego w następnym etapie modelowania, tzn. w etapie budowy modelu matematycznego.

Ogólna postać niezawodnościowego modelu obiektu technicznego

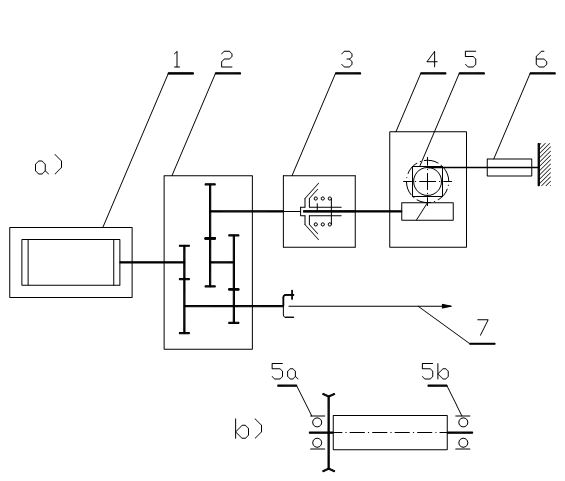
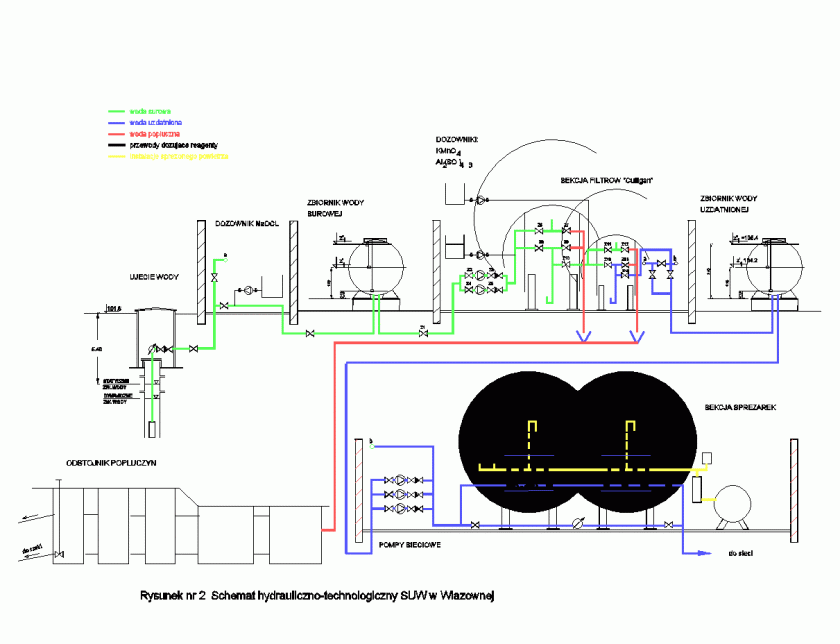
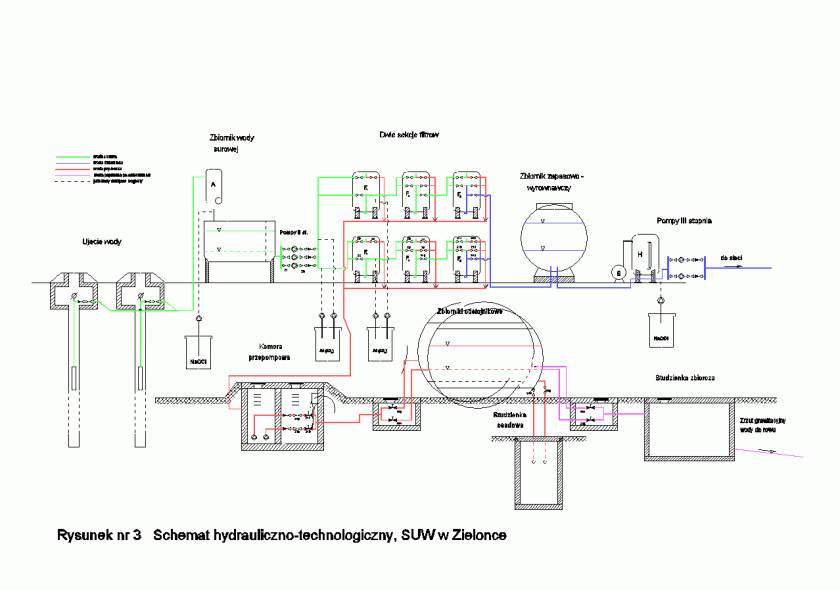
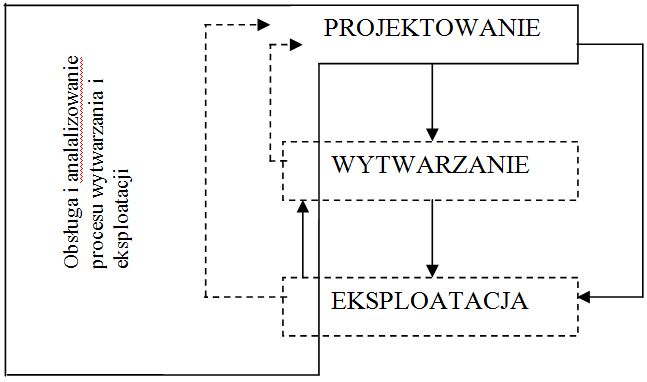
Przedstawianie poszczególnych elementów systemu racjonal­nego oddziaływania na niezawodność obiektu mechanicznego w fa­zie projektowania zacznijmy od sformułowania ogólnej postaci niezawodnościowego modelu obiektu.

Z punktu widzenia niezawodności proces eksploatacji obiek­tu mechanicznego charakteryzują trzy grupy czynników: zadanie (funkcja) Za(t)  przewidziane do wykonywania przy użyciu te­go obiektu, stan otoczenia Ot(t)  i sposób eksploatacji U(t). Każdy z tych czynników może być określony za pomocą odpowied­niego zbioru elementów (cech) istotnych ze względu na nieza­wodność, a bezpośrednio ze względu głównie na oddziaływania zewnętrzne.

Na przykład do zbioru elementów zadania Za(t),  przewi­dzianego do wykonania przy użyciu samojezdnego żurawia budow­lanego, można zaliczyć m.in.: odległość między kolejnymi miej­scami przenoszenia ładunków, masy i liczby przenoszonych ła­dunków, współrzędne ładunku przed przeniesieniem i po przenie­sieniu itd.

Eksploatacja obiektu mechanicznego przebiega w określonych warunkach zewnętrznych nazywanych otoczeniem. Oddziaływania otoczenia na obiekt zależą od stanu otoczenia Ot(t).  Elemen­tami stanu otoczenia na przykład w przypadku żurawia samojezd­nego są: agresywność chemiczna środowiska, prędkość wiatru, temperatura powietrza, intensywność zapylenia i zapiaszczenia powietrza itd.

Prócz otoczenia na obiekt oddziałuje również człowiek,  a ściślej – zespół ludzi sterujący jego eksploatacją. Grupa czynników, od których zależą te właśnie oddziaływania, to spo­sób eksploatacji U(t).  Elementy sposobu eksploatacji w przy­padku żurawia samojezdnego, to m.in.: czas przenoszenia ładun­ku, liczba i rodzaje ruchów wysięgnika przy przenoszeniu ładunku, błędy użytkowania (np. skośne ciągnięcie ładunku), okresy między odnowami profilaktycznymi elementów, jakość od­nów itd. W ogólnym przypadku zadanie  Za(t),  stan otoczenia Ot(t)  i sposób eksploatacji U(t)  mogą być traktowane jako wielowymiarowe procesy losowe.

Wymienione czynniki  (Za, Ot, U),  charakteryzujące proces eksploatacji, decydują o wartościach różnego rodzaju tzw. od­działywań zewnętrznych. Oddziaływania te można podzielić na dwie zasadnicze grupy : grupę oddziaływań otocze­nia, głównie mechanicznych i chemicznych (które mogą być opi­sywane za pomocą na przykład temperatury i ciśnienia powie­trza, prędkości wiatru itd.) zależnych od Ot  i grupę oddzia­ływań roboczych wynikających z czynności wykonywanych przez obiekt (np. obciążenia zewnętrzne), zależnych od Za ,Ot i U. Ponieważ każda z wielkości Za , Ot  i U zmienia się w czasie zwykle w sposób losowy, więc zbiór oddziaływań zewnętrznych Ga(t)  jest również wielowymiarowym procesem losowym. Z rozwa­żań tych wynika, że między Ga oraz Za , Ot i U istnieje związek, który można przedstawić w sposób ogólny za pomocą re­lacji

Ga(t)=g[Za(t), Ot(t), U(t)].                                                                             (2)

Oddziaływania zewnętrzne Ga(t)  są przyczyną pojawienia się pewnych zjawisk fizycznych, pod wpływem których ulegają zmianom w czasie (zwykle niekorzystnym) m.in. te własności obiektu, od których zależy jego prawidłowe funkcjonowanie. W przypadku obiektów mechanicznych są to zwykle własności geo­metryczne (np. luz, wielkość trwałego odkształcenia elementu itd.) i własności materiałowe (np. wytrzymałość doraźna, wy­trzymałość zmęczeniowa itd.) ich elementów. Zbiór wszystkich własności geometrycznych, materiałowych i innych obiektu me­chanicznego, istotnych z punktu widzenia niezawodności, zwany dalej stanem technicznym e(t)  obiektu, może być traktowany jako wielowymiarowy proces losowy, ponieważ wiele z tych włas­ności obiektu zmienia się w czasie jego eksploatacji w sposób losowy. Szybkość zmian stanu technicznego e(t)  pod wpływem oddziaływań zewnętrznych zależy nie tylko od poziomu tych od­działywań, ale także od wspomnianych własności obiektu w chwili początkowej  t = O,  czyli  od początkowego stanu technicz­nego eO.

Stan techniczny e (t)  obiektu w chwili  t  zależy więc od czasu, jaki upłynął od początku eksploatacji, od przebiegu oddziaływań zewnętrznych w całym przedziale czasu od O  do t  oraz od początkowego stanu technicznego. Ta ostatnia zależ­ność występuje szczególnie wyraźnie w przypadku obiektów me­chanicznych (np. zapas wytrzymałości zginanego wałka zależy od promienia zaokrąglenia odsądzenia). Każda składowa stanu tech­nicznego (np. luz) jest więc odpowiednim funkcjonałem, czyli

e(t) = f [Ga(t), eO, t]    dla   0 £ t £ t                                                              (3)

Od stanu technicznego obiektu zalezą bezpośrednio warto­ści przyjętych cech zdatności Zn(t),  gdzie v = 1,2,…,n, a n  jest liczbą tych cech. Cechy zdatności są to wielkości związane bezpośrednio ze stanem technicznym obiektu, nadające się do łatwego teoretycznego odwzorowywania zachodzących (w czasie) zmian zdolności obiektu do poprawnego funkcjonowa­nia. Decydują więc one o tzw. stanie niezawodnościowym obiek­tu (zdatny, niezdatny). Cechami zdatności elementu obiektu mechanicznego mogą być na przykład zapas uogólnionej wytrzy­małości, skumulowane względne uszkodzenie zmęczeniowe,  po­wierzchniowy ubytek materiału, luz itd.  Każda z cech zdatności obiektu zależy nie tylko od stanu technicznego e(t) obiektu w chwili  t,  lecz także od poziomu oddziaływań ze­wnętrznych Ga(t)  w tej chwili: Na przykład zapas uogólnio­nej wytrzymałości doraźnej przekroju elementu obiektu mecha­nicznego Z (t) =W(t) – cO(t)  zależy od uogólnionej wytrzy­małości  W (stan techniczny) i od uogólnionego obciążenia O (oddziaływanie zewnętrzne). Można więc te zależności ująć  w sposób ogólny za pomocą relacji

Zn(t) = jn[e(t), Ga(t)]     dla n = 1, 2 ,…, n.                                                    (4)

Wartości tych cech zdatności, jak wynika ze związków (3) i (4), zmieniają się w czasie eksploatacji obiektu wskutek występowania oddziaływań zewnętrznych. Są to zwykle zmiany niekorzystne polegające na zbliżaniu się wartości tych cech do przyjętych granicznych wartości  Zngrd  lub  Zngrg    (n = 1, 2,…, n)  ograniczających obszar zdatności Wz.

Jeżeli stan wszystkich cech zdatności obiektu w danej chwili  t należy do obszaru Wz ,  to obiekt jest zdatny do poprawnego funkcjonowania, czyli znajduje się w stanie zdatności. W przypadku obiektów mechanicznych zachodzi to na ogół wtedy, gdy spełnione są jednocześnie następujące relacje

Zngrd £ Zn(t) £ Zngrg         dla n = 1, 2 ,…, n.                                                    (5)

Na wiele cech zdatności obiektu mechanicznego mogą być na­kładane tylko ograniczenia jednostronne, ale takie przypadki zawarte są w ogólnych warunkach (5) ograniczających obszar Wz .

Jeśli co najmniej jedna z cech zdatności  Zn(t)  obiektu wyjdzie wskutek zmian jego stanu technicznego  e(t)  poza ob­szar Wz ,  to zdarzenie takie oznacza pojawienie się niespraw­ności. Czas  T,  jaki upłynął od początku eksploatacji do chwili pojawienia się niesprawności jest zmienną losową, po­nieważ każda z cech zdatności Zn(t)  jest procesem losowym.

Relacje (2) – (5)  tworzą najogólniejszą postać niezawod­nościowego modelu obiektu. Jego rozwiązanie prowadzi do okre­ślenia zależności odpowiednich wskaźników niezawodności od różnych czynników konstrukcyjnych i technologicznych (opisa­nych przez eO. )  oraz eksploatacyjnych (opisanych przez wiel­kości Za ,Ot  i U  określające proces eksploatacji). Jeśli na przykład miarą poziomu niezawodności jest funkcja niezawod­ności  R(t),  to wspomniana zależność R(t)  od czynników kon­strukcyjnych, technologicznych i eksploatacyjnych wynika z re­lacji

R(t) = P{[ Z1grd £ Z1(t) £ Z1grg ]  [ Z2grd £ Z2(t) £ Z2grg ] …. [ Zngrd £  Zn(t) £ Zngrg ]}                                                                                                                        (6)

oraz z relacji (2) – (5). Postać ogólna tej zależności może być przedstawiona na przykład następująco

R(t) = y1[ Za(t), Ot(t), U(t); eO; t]    dla  0 £ t £ t                                        (7)

lub w przypadku innych wskaźników niezawodności również w po­staci

R(t) = y2[ Ga(t); U(t); eO; t]    dla  0 £ t £ t                                                   (8)

co wynika m.in. z relacji (2) – (6). Wyrażenia (7) i (8) aa słuszne dla większości używanych wskaźników niezawodności, dlatego symbol  R(t)  jest w nich l w dalszej części tekstu traktowany jako uogólniony wskaźnik niezawodności (prócz tych przypadków, w których wyraźnie nazywa się go funkcją niezawod­ności).

Uwzględnione w wyrażeniach (7) i (8) czynniki konstrukcyj­ne i technologiczne (opisane przez eO )  oraz eksploatacyjne (opisane przez Za , Ot i U )  są zwykle modelowane w procesie konstruowania za pomocą zbiorów wielkości zdeterminowanych i parametrów zmiennych losowych. Zbiory te zostały oznaczone w rozdz. 2 symbolami  ck, ct i ce .  Zależność poziomu niezawod­ności od tych czynników można więc przedstawić w jeszcze innej postaci ogólnej, danej relacją (1).

Relacje (1) oraz (7) i (8) wskazują, że przez odpowiedni dobór wartości tych czynników, np. wymiarów i kształtów ele­mentów, rodzajów materiałów, dokładności obróbki, częstości odnów profilaktycznych itd., można oddziaływać na niezawod­ność obiektu już w fazie jego konstruowania. Aby to oddziały­wanie mogło być racjonalne, należy przedtem przeprowadzić teoretyczne badania niezawodności w celu określenia wpływu tych różnych czynników na niezawodność tworzonego obiektu. Takie badania niezawodności konkretnego obiektu mechanicznego możliwe są jednak wówczas, gdy znana jest szczegółowa postać niezawodnościowego modelu tego obiektu, a więc szczegółowe po­stacie relacji (2) – (5) oraz gdy znane są potrzebne dane (np. o stanie początkowym eO ).  Zasady tworzenia takiej postaci modelu przedstawione są w rozdziale następnym, natomiast ogólna postać modelu (relację (2) – (5)) oraz wprowadzone po­wyżej pojęcia i symbolika zostaną wykorzystane w rozdz. 5 do zaprezentowania teoretycznych metod badań niezawodności obiek­tów.

Cel i zakres pracy magisterskiej

Z wymienionych powyżej powodów za cel niniejszej pracy przyjęto opracowanie systemu racjonalnego oddziaływania na niezawodność obiektu technicznego w fazie jego projektowania. System ten ma być tym narzędziem, za pomocą którego można oddziaływać na niezawodność projektowanego obiektu w sposób bardziej racjonalny niż za pomocą stosowanych powszechnie deterministycznych metod . projektowania

Celem stosowania tego systemu jest doskonalenie pod wzglę­dem niezawodności rozwiązania konstrukcyjnego obiektu i ewentualnie sposobów jego wytwarzania i eksploatacji. Podstawą do wprowadzenia ulepszeń są wyniki badań niezawodności (głównie teoretycznych) tworzonego obiektu. Teoretyczne badania nieza­wodności polegają na wyznaczeniu zależności przyjętych wskaź­ników niezawodności  R  od zbioru czynników konstrukcyjnych ck,  technologicznych  ct  oraz eksploatacyjnych  ce

R = y[ck, ct, ce, (t)]    dla  0 £ t £ t                                                                (1)

oraz na analizie wpływu tych czynników na poziom niezawodności [19]. Czynniki konstrukcyjne  ck,  to: własności geometryczne (kształty, wymiary, dokładności wymiarów itd.), własności materiałów elementów i elementów (rodzaje materiałów, ich włas­ności fizyczne, w tym wytrzymałość mechaniczna, przewodność elektryczna, cieplna itd.) i inne, np. ergonomiczne. Czynniki technologiczne  ct,  to m.in. kwalifikacje bezpośrednich wy­konawców, rodzaje i stan techniczny obrabiarek, jakość kontro­li procesu wytwarzania itd., natomiast czynniki eksploatacyjne, to sposób eksploatacji (m.in. częstość przeglądów,  częstość odnów profilaktycznych), oddziaływania robocze (obciąże­nia zewnętrzne, czas eksploatacji itd.), stan otoczenia.

Wspomniane badania niezawodności w fazie projektowania są głównie badaniami teoretycznymi, przeprowadzanymi na odpowied­nich teoretycznych (abstrakcyjnych) modelach obiektów, bo obiektów materialnych jeszcze w tej fazie nie ma albo ich liczba nie jest wystarczająca do eksperymentalnych badań nie­zawodności. Badania takie wymagają więc uprzedniego zbudowania niezawodnościowego modelu projektowanego obiektu.

W ogólnym przypadku model niezawodnościowy obiektu (zarów­no teoretyczny, jak i materialny) jest to układ, który pod względem niezawodności odwzorowuje obiekt rzeczywisty, uwzględ­niając pewne stany i procesy występujące w obiekcie oraz w je­go otoczeniu, istotne z punktu widzenia niezawodności. W przy­padku modelu teoretycznego (abstrakcyjnego) tym układem jest zwykle zbiór relacji matematycznych i występujących w nich wielkości, opisujący te stany oraz procesy i wystarczający do określenia poziomu niezawodności badanego obiektu.

Wyniki badań niezawodności mogą być podstawą do typowania najkorzystniejszych rodzajów ulepszeń, wprowadzanych w różnych etapach fazy konstruowania. W tej fazie najbardziej efektywnie mogą być one wykorzystane w etapach opracowania projektu wstępnego oraz projektu technicznego, prócz tego w etapach ulepszania rozwiązania obiektu po eksperymentalnych badaniach prototypu i serii informacyjnej.

A więc do działań wchodzących w skład systemu racjonalnego oddziaływania na niezawodność należy zaliczyć przede wszyst­kim:

  • budowa niezawodnościowego modelu obiektu,
  • badania niezawodności, głównie badania teoretyczne prze­prowadzane na zbudowanym modelu,
  • typowanie najkorzystniejszych rodzajów ulepszeń: rozwią­zania projektowego, procesu wytwarzania oraz procesu eks­ploatacji. W skład systemu wchodzą prócz tego zasady i sposoby tych działań.

Przeznaczeniem proponowanego systemu racjonalnego oddzia­ływania na niezawodność obiektu nie jest zastępowanie,  lecz głównie wspomaganie stosowanych powszechnie metod projektowania oraz eksperymentalnych metod badań prototypów, serii in­formacyjnej i produkowanych obiektów.

Najważniejszym i najtrudniejszym z działań wchodzących w skład systemu jest tworzenie niezawodnościowego modelu obiek­tu. Zagadnieniom niezawodnościowego modelowania obiektów me­chanicznych poświęcone są dwa następne rozdziały niniejszego opracowania (rozdz. 3 i 4). W rozdziale 3 jest przedstawiona ogólna postać niezawodnościowego modelu obiektu mechanicznego, niezależna od rodzaju obiektu. Zbiór relacji, które ją tworzą, może być też traktowany jako ogólny opis procesu powstawania niesprawności obiektu mechanicznego.

W dalszej części pracy zamiast terminu „uszkodzenie” używa się bardziej ogólnego terminu „niesprawność”. Uszkodzeniem nazywa się tylko taką niesprawność, która uniemożliwia funkcjonowanie obiektu w sposób fizyczny (nie umowny). Definicja niesprawno­ści obiektu mechanicznego zostanie podana w p. rozdz. 4.2.

Do badań niezawodności konkretnego obiektu, o przyjętym rozwiązaniu technicznym, konieczne jest utworzenie szczegóło­wej postaci modelu niezawodnościowego tego obiektu. Budowanie takiej postaci modelu odbywa się w dwóch etapach. W pierwszym z nich powstaje tzw. model nominalny (fizyczny), jako rezultat przyjęcia zasadniczych założeń upraszczających, które polegają głównie na pominięciu mniej istotnych zjawisk fizycznych pro­wadzących do niesprawności obiektu. W drugim etapie powstaje model matematyczny, czyli wspomniany już zbiór relacji stano­wiących matematyczny opia stanów i procesów decydujących o po­ziomie niezawodności projektowanego obiektu.

Zbiór relacji tworzących model może być podstawą do wyzna­czenia zależności przyjętego wskaźnika niezawodności od róż­nych czynników projektowych, technologicznych i eksploata­cyjnych (p. wyrażenie (1)).

Rozdziały 3-5 prezentują więc pierwsze dwa elementy (działania) proponowanego systemu. Przedstawione w nich zasa­dy i sposoby tych działań można uznać za podstawy teoretycz­nych badań niezawodności obiektu mechanicznego, ułatwiających racjonalne oddziaływanie na tę niezawodność już w fazie projektowania obiektu.

Metoda oceny parametrów niezawodnościowych oraz kosztów eksploatacji złożonych systemów, nie wymagająca przyjmowania założeń upraszczających charakterystycznych dla metod Markowa została ujęta w rozdziale 6.

Rozdział 7 przedstawia model matematyczny kształtowania niezawodności obiektu w procesie projektowania i badań.

W kolejnym 8 rozdziale omówiono modelowanie cech zdatności elementów maszyn.

Wyniki teoretycznych badań niezawodności są podstawą do wprowadzenia ulepszeń rozwiązania konstrukcyjnego i ewentualnie sposobów wytwarzania i eksploatacji obiektu. Zasady typowania najkorzystniejszych rodzajów tych ulepszeń, a więc zasady trzeciego z podstawowych działań proponowanego systemu oddziaływania na niezawodność obiektu, są zaprezentowane w rozdz. 9. W rozdziale tym są też przedstawione sposoby i możliwości wykorzystania tego systemu głównie w fazie projektowania.

W rozdziale 10 przedstawiono  sposób przeprowadzania obliczeń niezawodnościowych w fazie projektowania na przykładzie obrotowej wiertarki elektrycznej wg. metody LEMACH.

Ocena niezawodności urządzenia w fazie projektowania na przykładzie obrotowej wiertarki elektrycznej

[z pracy magisterskiej]

W niniejszym rozdziale przedstawiono sposób przeprowadzania obliczeń niezawodnościowych w fazie projektowania urządzeń technicznych wg metody projektowania LEMACH 2 [8], ze względu na podatność jej struktury na rozgałęzienia algorytmów.

Wybór rodzaju obliczeń niezawodności, których należy dokonać na kilku etapach projektowania, uzależniony jest od fazy przybliżenia projektowego (tabela. 1).

Ze względu na podobieństwo toku obliczeń odpowiadających poszczególnym etapom projektowania, podjęto próbę algorytmizacji działań prowadzących do oceny niezawod­ności urządzenia.

Proponowany algorytm ma charakter ogólny i może być wykorzystany w innych me­todach projektowania.

Sposób przeprowadzenia obliczeń niezawodnościowych wg zaproponowanego algo­rytmu przedstawiono na przykładzie orientacyjnej oceny niezawodności projektu wstęp­nego (etap III wg tab. 1) obrotowej wiertarki elektrycznej.

Algorytm oceny niezawodności projektowanych urządzeń technicznych:

  1. Dokonaj podziału projektowanego urządzenia na elementy. Podział przeprowadź w stopniu szczególności zależnym od fazy przybliżenia projektowego.
  1. Zidentyfikuj strukturę niezawodnościową urządzenia przy zastosowaniu jednej z podanych metod:

a) diagnostyki technicznej i zasad budowy testów rozpoznających stan niezawodności,

b) symulacyjnej,

i określ wzorem niezawodność strukturalną urządzenia.

Przy małym stopniu skomplikowania urządzenia identyfikacja nie wymaga stosowania wymienionych metod.

Zależność rodzaju obliczeń niezawodnościowych od etapu projektowania

(tabeli 1)

Etap projektowania  Czynności projektowe

wg.  metody „LEMACH 2”

  Rodzaj obliczeń niezawodnościowych
I Rozpoznawanie potrzeb,

formułowanie problemu
II Tworzenie i wybór koncepcji rozwiązania projektowego Określenie wymagań niezawodnościowych dla projektowanego urządzenia np. w postaci prawdopodobieństwa poprawnej pracy, lub średniego czasu poprawnej pracy.

Szacowanie wskaźników niezawodnościowych dla n koncepcji urządzenie ( przy wyborze koncepcji optymalnej należy uwzględnić kryterium niezawodności)
II Opracowanie syntezy, projekt wstępny Orientacyjne obliczenie niezawodności (nie ma jeszcze pełnych informacji o parametrach i warunkach pracy poszczególnych  elementów urządzenia, znana jest struktura tj. liczba elementów i współzależności między nimi)
IV Opracowanie rozwiązania szczegółowego i ocena rozwiązania Dokładne obliczenia niezawodności z uwzględnieniem warunków pracy i dodatkowych czynników zależnych od przyjętych szczegółowych rozwiązań konstrukcyjnych
V Realizacja próbna projektu.

Badania, opracowanie wniosków,

danych technologicznych i eksploatacyjnych

 Eksperymentalna ocena niezawodności.

Wykrycie elementów o niedostatecznej niezawodności, wprowadzenie odpowiednich korekt w końcowe obliczenia i  koniecznych zmian konstrukcyjnych
  1. Zbierz informacje niezawodnościowe o elementach:

a) z literatury, katalogów, norm – o postaciach i, parametrach rozkładów funkcji niezawodności, wyodrębnionych elementów urządzenia,

b) z banku informacji – o uszkodzeniach elementów urządzenia (o postaciach uszko­dzeń, o średnich czasach pracy bezawaryjnej itp.)

c) w przypadku braku danych o uszkodzeniach wyodrębnionych elementów urządzenia  – przyjmij dane niezawodnościowe elementów o podobnej konstrukcji, technologii i zastosowaniu, lub – wykorzystaj posiadane informacje niezawodnościowe o elementach wyższego, względnie niższego rzędu w stosunku do wyodrębnionych, lub – zleć przeprowadzenie niezawodnościowych badań konstrukcyjnych wyodrębnio­nych elementów urządzenia

UWAGA:

Jeżeli w kroku 3 algorytmu postąpiłeś zgodnie z 3a, pomiń kroki 4, 5 i 6.

  1. Wyznacz modele matematyczne rzeczywistych rozkładów uszkodzeń elementów, stosując
  • metodę analizy statystycznej, lub
  • metodę graficzną.

Wykorzystaj fakt, że najczęściej występującymi rozkładami czasu poprawnej pracy są rozkłady: wykładniczy, normalny, logarytmo-normalny, Weibulla.

  1. Wyznacz parametry otrzymanego rozkładu korzystając z:
  • metody najmniejszych kwadratów,
  • metody największej wiarygodności, lub
  • tablic siatki prawdopodobieństwa rozkładu.
  1. Zweryfikuj przyjęte modele matematyczne rzeczywistych rozkładów uszkodzeń elementów przy pomocy wybranego testu zgodności: Kołmogorowa, Pearsona, Hartley’a, c – kwadrat.
  1. Oblicz wartości funkcji niezawodności poszczególnych elementów urządzenia. Wyniki obliczeń zestaw w tabeli oraz przedstaw graficznie przebiegi funkcji nieza­wodności.
  1. Oblicz niezawodność strukturalną projektowanego urządzenia.

UWAGA:

Krok 8 kończy ocenę niezawodności dla etapów II i III projektowania urządze­nia wg metody LEMACH 2.

  1. Przeprowadź ocenę wyników szacowania niezawodności oraz ich i interpretację przy pomocy analizy wariancji, analizy regresji lub analizy spektralnej.
  1. W oparciu o uzyskane wskaźniki niezawodnościowe zaakceptuj projekt urządzenia lub ustal przesłanki do jego modyfikacji.

UWAGA:

Jeżeli do oceny niezawodności wybrałeś metody symulacyjne, dokonaj optyma­lizacji urządzenia wg kryteriów niezawodności.

Orientacyjna ocena niezawodności urządzenia na etapie III projektowania wg metody Lemach 2:

Wstępne określenie niezawodności projektowanego urządzenia przeprowadza się przy pomocy przybliżonych obliczeń, opartych na następujących założeniach:

  • uszkodzenia elementów są zdarzeniami losowymi, wzajemnie niezależnymi,
  • rozpatrywane są jedynie elementy wchodzące w skład zasadniczego układu funkcjo­nalnego,
  • warunki pracy nie mają wpływu na niezawodność urządzenia.

Szacowanie niezawodności wg zaproponowanego algorytmu przeprowadzono dla szlifierki kątowej.

  1. Podział projektowanego urządzenia na elementy przedstawiono na rysunku 1.

1 – silnik,

2 – reduktor,

3 – sprzegło,

4 – przekładnia ślimakowa,

5 – bęben,

6 – lina.

rysunek-do-pracy2Rys. 9. Obrotowa wiertarka elektryczna do pracy z podpory z posuwowym mechanizmem kołowrotowym:

  1. schemat kinematyczny, b) sposób łożyskowania bębna:

1 – silnik, 2 – reduktor, 3 – sprzęgło, 4 – przekładnia ślimakowa, 5 – bęben,

5a, 5b – łożyska bębna, 6 – lina, 7 – wiertło

  1. Identyfikacja struktury niezawodnościowej urządzenia oraz określenie niezawodności strukturalnej.

Wiertarka posiada szeregową strukturę niezawodnościową, którą przedstawiono na rysunku 10.

rysunek-do-pracy1Rys. 10. Schemat struktury niezawodnościowej wiertarki

Symulacyjne metody badań niezawodności

Metoda symulacji rozwinęła się najpierw w teorii systemów ekonomicznych i systemów zarządzania. Metoda ta może być z dużym powodzeniem stosowania również do badań niezawodności obiektów technicznych, m.in. mechanicznych. Jednakże przedstawione w tych pracach me­tody symulacji dotyczą jedynie niektórych części modelu nie­zawodnościowego obiektu technicznego, zwykle procesu eksploa­tacji lub są wykorzystywane do wyznaczania wskaźników nieza­wodności obiektu złożonego przy danych wskaźnikach niezawodno­ści jego elementów. Są to badania o małej przydatności dla konstruktora, zwłaszcza obiektów mechanicznych. Zdecydowanie .więcej informacji korzystnych dla konstruktora obiektu mecha­nicznego dają badania niezawodności oparte na pełnej postaci niezawodnościowego modelu obiektu, przedstawionej w rozdz. 4. Próby zastosowania metody symulacji do takich badań niezawodności obiektów mechanicznych przedsta­wione są w pracach [12, 24, 26]

W przypadku badań niezawodności obiektu mechanicznego me­toda symulacji jest to technika numeryczna, polegająca na na­śladowaniu stanów i procesów decydujących o niesprawnościach obiektu i ujętych w modelu niezawodnościowym.

PROBLEMY WSPOMAGANIA DECYZJI W PROCESIE PROJEKTOWANIA SYSTEMÓW Z UWZGLĘDNIENIEM ASPEKTÓW NIEZAWODNOŚCI

Decyzje, jakie ma do podjęcia projektant współczesnych systemów tech­nicznych, wymagają uwzględnienia wielu uwarunkowań i spełnienia niejedno­krotnie sprzecznych wymagań. Jednym z istotnych czynników jest ogólnie ro­zumiana niezawodność systemu. Zazwyczaj niezawodność nie jest oczywiście najważniejszym kryterium, które wpływa na podstawowe decyzje projektowe, bywa jednak w wielu przypadkach ważnym kryterium pomocniczym. Z tego względu ilościowa informacja dotycząca charakterystyk niezawodności projek­towanego systemu jest ważna i umożliwia sensowne wspomaganie podejmowa­nia decyzji, które w przyszłości, a więc w czasie eksploatacji systemu mogą mieć znaczne skutki ekonomiczne. Przykładem może być zadanie organizacji serwisu elementów systemu. Na wstępie należy podjąć decyzję, czy serwis ma być przeprowadzany samodzielnie przez eksploatującego system, czy przez ze­wnętrznego dostawcę usług serwisowych. W przypadku wyboru pierwszego wariantu konieczne jest dalej przykładowe określenie liczby ekip naprawczych. W wariancie drugim, gdy zdecydowano się na serwis zewnętrzny, należy zdecy­dować, jakie powinny być warunki umowy zawieranej z dostawca usług. W podjęciu dobrej decyzji pomaga oczywiście właściwe i w miarę formalne postawienie problemu. W rozważanym zadaniu może to być na przykład wyma­ganie zapewnienia określonego poziomu niezawodności systemu, wyrażanego np. zadanym współczynnikiem gotowości, przy minimalnym koszcie napraw. Nie wdając się w szczegóły dotyczące technik optymalizacji, rozwiązanie tak postawionego zadania polega zwykle na sprawdzeniu pewnej liczby wariantów organizacji serwisu i wybraniu najtańszego wśród tych, dla których projektowa­ny system spełnia założone wymagania niezawodnościowe. Jednak odpowiedź na pytanie, jaki jest współczynnik gotowości systemu nie jest w praktyce wcale taka prosta. Wyliczenie współczynnika wymaga po pierwsze przyjęcia właści­wego modelu matematycznego systemu, a następnie, aby uzyskać wynik liczbowy, dostarczenia w miarę wiarygodnych danych o elementach systemu. Sam sposób prowadzenia obliczeń jest kwestią drugorzędną. Modele rozważane od lat w literaturze dotyczącej teorii niezawodności czy teorii obsługi masowej, oparte z reguły na teorii procesów Markowa czy półmarkowa, są bardzo często wyidealizowane i trudne do pogodzenia z praktyką. Rozważa się zazwyczaj stosunkowo proste struktury niezawodnościowe i przyjmuje ostre założenia co do rozkładów zmiennych losowych opisujących czasy życia elementów systemu i czasy ich napraw. Podyktowane to bywa często chęcią uzyskania eleganckich z matematycznego punktu widzenia rozwiązań analitycznych, a także pewnym, jak się wydaje, przywiązaniem do opanowanego aparatu analizy. Istnieją oczy­wiście próby analizy za pomocą tych klasycznych metod struktur bardziej zło­żonych niż szeregowo-równo ległe czy k z n, lecz pojawia się wtedy zwykle problem nadmiernego wzrostu liczby stanów systemu. Znaczną z punktu widze­nia praktyki niedogodnością jest też konieczne w większości wyżej wspomnia­nych modeli założenie o wykładniczości wszystkich czy prawie wszystkich roz­kładów zmiennych losowych. W praktyce utrzymanie w mocy takiego założenia jest nie do przyjęcia w przypadkach, gdy na podstawie wcześniej wykonanych badań niezawodnościowych wynika, że rozkład jest znacząco inny.

Przebieg procesu modelowania

Tworzenie szczegółowej postaci niezawodnościowego modelu obiektu mechanicznego możliwe jest na ogół dopiero wówczas, gdy znane jest co najmniej wstępne rozwiązanie konstrukcyjne badanego obiektu, powstałe na przykład przy użyciu tradycyj­nych metod konstruowania. Dopiero wtedy bowiem możliwe jest m.in. utworzenie zbioru informacji o początkowym stanie tech­nicznym eO) ,  a więc o kształtach i wymiarach elementów, o wy­trzymałościowych własnościach elementów itd. Metoda teoretycz­nych badań niezawodności jest więc metodą wspomagającą i wery­fikującą tradycyjne metody konstruowania. Może ona dostarczyć informacji na przykład o prawdopodobieństwie uszkodzenia kon­struowanego obiektu w założonym okresie eksploatacji oraz in­formacji o sposobach zwiększania tego prawdopodobieństwa.

Przebieg budowy szczegółowej postaci niezawodnościowego modelu obiektu mechanicznego jest zgodny ze znanym przebiegiem procesu modelowania w technice w ogóle. Tak na przykład przed etapem tworzenia modelu nominalnego i przed etapem tworzenia modelu matematycznego konieczne jest zgromadzenie wielu in­formacji o modelowanym obiekcie. Informacje te uzyskuje się z etapu konstruowania metodami tradycyjnymi i na podstawie do­świadczenia zgromadzonego przy wytwarzaniu i eksploatacji obiektów podobnych) oraz w wyniku eksperymentalnych badań elementów i materiałów, z których będzie zbudowany modelowany obiekt itd.

Przed przystąpieniem do budowy modelu nominalnego nale­ży zebrać te informacje, które mogą być podstawą do wprowadze­nia zasadniczych założeń, upraszczających rzeczywistość przy jej opisie za pomocą modelu. Są to więc przede wszystkim in­formacje o procesie eksploatacji, decydującym o oddziaływa­niach między otoczeniem i obiektem; o zjawiskach fizycznych przebiegających w obiekcie wskutek tych oddziaływań; o posta­ciach i skutkach ewentualnych uszkodzeń elementów; o wpływie uszkodzeń elementów lub ich fragmentów na stan zdatności całego obiektu. Im więcej zgromadzi się takich informacji o obiek­cie, tym łatwiej można zbudować jego model i tym lepiej model ten może odwzorowywać badany obiekt.

Następnym krokiem jest analiza uzyskanych informacji w ce­lu sklasyfikowania ich pod względem ważności z punktu widzenia niezawodności badanego obiektu.

Po przeprowadzeniu tej analizy przystępuje się do budowy modelu nominalnego. Jest to bardzo ważny etap procesu modelo­wania, w nim bowiem przyjmuje się zasadnicze założenia upra­szczające rzeczywistość, polegające przede wszystkim na pomi­nięciu mniej istotnych procesów prowadzących do niesprawności i na uwzględnieniu w modelu tylko tych fragmentów obiektu, które są najbardziej narażone na niesprawności (w tym uszko­dzenia). Te fragmenty obiektu nazywa się dalej punktami kon­trolnymi (PK)[24]. Punktami kontrolnymi są na przykład takie frag­menty elementów obiektów mechanicznych, które w metodach obli­czeń stosowanych przez konstruktorów są modelowane za pomocą tzw. przekrojów, punktów powierzchni itd. W pewnych przypad­kach mogą to być całe elementy lub nawet grupy elementów, opi­sywane tymi samymi wspólnymi cechami zdatności, takimi jak na przykład luz, opory ruchu lub sprawność mechaniczna.

W etapie budowy modelu nominalnego określa się też gra­niczne stany techniczne poszczególnych PK i całego obiektu, oddzielające odpowiednie stany zdatności od stanów niezdatności. Definiuje się więc zdarzenia powstania niesprawności tych PK i całego obiektu. Pozwala to m.in. na podjęcie decyzji co do tzw. struktury niezawodnościowej obiektu.

Przed przystąpieniem do budowy modelu matematycznego konieczne jest zgromadzenie dalszych informacji o obiekcie, tym razem tych, które są potrzebne do matematycznego opisu powstałego modelu nominalnego czyli do matematycznego opisu stanów i procesów decydujących o niesprawnościach obiektu, uwzględnionych przez model nominalny. Przede wszystkim są to informacje: o postaciach matematycznych i parametrach rozkła­dów zmiennych losowych opisujących własności geometryczne, wytrzymałościowe i inne obiektu w punktach kontrolnych, wybra­nych przy budowie modelu nominalnego; o postaciach matematycz­nych i parametrach procesów losowych opisujących eksploatację obiektu, jego obciążenia zewnętrzne oraz wewnętrzne zjawiska fizyczne uwzględnione przez model nominalny, prowadzące do niesprawności PK; o zależnościach stochastycznych między tymi zjawiskami fizycznymi.

Zbiór takich informacji jest podstawą do utworzenia modelu matematycznego, czyli tej postaci modelu, która bezpośrednio jest wykorzystywana w późniejszych teoretycznych badaniach niezawodności. Przy tworzeniu modelu matematycznego wprowadza się dalsze założenia upraszczające, jednakże dotyczą one już tylko opisu matematycznego tego, co uwzględnia model nominalny.

W następnych dwóch podrozdziałach (4.2 i 4.3) zostaną przedstawione ogólne zasady budowy szczegółowych postaci niezawodnościowych modeli obiektów mechanicznych w odniesieniu do obydwu głównych etapów procesu modelowania – budowy modelu nominalnego i budowy modelu matematycznego.

[będziemy jeszcze pisać o tej pracy]

Opis cyklu hydraulicznego pracy układu

Stacja wodociągowa zrealizowana została na podstawie dokumentacji wykonanej w 1971 r. przez WBPBO w Warszawie. Modernizacji dokonano na podstawie dokumentacji wykonanej przez Spółdzielnie Pracy „Expo-Service” w Poznaniu. Ostatecznie stację oddano do użytku w 1991 r. Stacja zasila w wodę budynki uczelniane i mieszkaniowe SGGW przy ulicy Nowoursynowskiej.

Stacja wodociągowa posiada dwa niezależne ujęcia wody:

1) czwartorzędowej – w skład którego wchodzą dwie studnie głębinowe nr 1a i 2a (spąg warstwy    wodonośnej 30 m poniżej terenu, a zwierciadło statyczne 10,8 m poniżej    terenu)

2)  trzeciorzędowej – w skład którego wchodzi jedna studnia głębinowa nr 3 (spąg warstwy    wodonośnej 265 m poniżej terenu, a zwierciadło statyczne 17,5 m poniżej    terenu).

Ujęcie wód czwartorzędowych jest podstawowym Ÿródłem wody zasilającej uczelnię, natomiast ujęcie wód oligoceńskich jest układem dodatkowym podłączonym do dwóch punktów czerpalnych o małej wydajności.

Opis cyklu hydraulicznego pracy układu czwartorzędowego.

W obu studniach zainstalowane są pompy głębinowe GRUNDFOSA typu SP 45/6 o następujących parametrach:

Q=22 ÷ 56 m3/h,

H=59 ÷ 24 m,

N=7,5 kW.

Zgodnie z rysunkiem nr 4, każda z pomp pompuje wodę na oddzielną sekcję filtracyjną. W sekcji woda przechodzi kolejno przez areator, odżelaziacz i odmanganiacz, oba o pojemności całkowitej 10 m3 . Po uzdatnieniu woda gromadzona jest w dwukomorowym żelbetowym zbiorniku zapasowo-wyrównawczym o pojemności 2*500m3. Ze zbiornika woda tłoczona jest do sieci trzema pompami typu 65 PJM 200 o następujących parametrach:

Q=24 ÷ 42 m3/h,

H=52 ÷ 40 m,

N=11 kW.

Na stanowisku pomp II stopnia znajduje się jeszcze jedna pompa zapasowa tego samego typu. Pracą pomp sterują dwa hydrofory o pojemności 10 m3 każdy. Układ płuczny składa się z trzech pomp typu 100 PJM 200 o następujących parametrach:

Q=42 ÷ 75 m3/h,

H=11,8 ÷ 9,5 m,

N=3 kW.

Jedna sekcja płukana jest z częstotliwością raz na trzy doby. Podczas płukania pracują dwie pompy płuczne, płucząc kolejno odżelaziacz a następnie odmanganiacz. Wody popłuczne spływają grawitacyjnie do odstojnika, z którego są spuszczane do kanalizacji.

Opis cyklu hydraulicznego pracy układu oligoceńskiego.

Układ jest jedno stopniowy zasilany pompą głębinową typu SIGMA UV N-1-6 o następujących parametrach:

Q=6 m3/h,

N=2,2 kW.

Pompa głębinowa transportuje wodę ze studni nr 3 przez areator do filtru odżelaziającego o pojemności całkowitej 10 m3. Po uzdatnieniu woda gromadzi się w hydroforze o pojemności 10 m3 skąd odpływa do sieci. Filtr ten jest płukany raz na tydzień.

W hali znajdują się dodatkowo jeden odmanganiacz i jeden odżelaziacz, które obecnie pełnią funkcję zapasowych.

Układ sprężonego powietrza, zasilający całą stację, składa się ze stanowiska sprężarek, zbiornika powietrza umieszczonego poza budynkiem stacji oraz armatury kontrolno-pomiarowej. Stanowisko sprężarek składa się ze sprężarki typu A50-380-240, ze wspomaganiem małą sprężarką typu 2 CV. Na wypadek awarii są dodatkowo dwie sprężarki.

wiazowna

zielonka

Niezawodność modeli urządzenia

na początek praca magisterska z Wydziału Mechanicznego

Poziom niezawodności obiektu jest kształtowany we wszyst­kich fazach powstawania i istnienia tego obiektu, tzn. w fa­zach projektowania, wytwarzania i eksploatacji.

Największe możliwości oddziaływania na niezawodność obiek­tu mechanicznego występują w fazie jego projektowania, a zwłaszcza w etapach jego kształtowania, tzn. tworzenia pro­jektu koncepcyjnego, projektu wstępnego i projektu technicznego.

W tej fazie bowiem wpływa się na niezawodność projektowanego obiektu m.in. przez dobór jego struktury funkcjonalnej; kształtu, wymiarów i materiałów elementów, obróbki cieplno-chemicznej, dokładności wykonania itd., co decyduje o pozio­mach wytężenia w różnych fragmentach konstrukcji i o przebie­gu procesów starzenia.

Probabilistyczne metody obliczeń wytrzymałościowych, nadające się ewentualnie do analizy niezawodności, dotyczą tylko jednego fragmentu kon­strukcji narażonego na uszkodzenie. Tylko nieliczne opracowania naukowe przedstawiają sposoby analizy niezawodności pewnych obiektów mechanicznych złożonych z wielu elementów (więcej niż l). Niektóre z nich, prezentują metody, które mogą być wykorzystane przy budowie struktur niezawodnościowych takich obiektów. Są to mię­dzy innymi metody dekompozycji i hierarchizacji elementów.

Inne, przedstawiają metody badań niezawodnościowych struktur obiektów, między innymi metody minimalnych ścieżek i minimalnych przekrojów. Należy podkreślić, że autorzy tych prac koncentrują się na budowie i badaniach niezawodnościo­wych struktur obiektów, a przedstawiane przez nich metody są oparte na założeniu znajomości niezawodności elementów obiek­tu. Podobne metody są stosowane do analizy niezawodności obiek­tów elektrycznych i elektronicznych. Dla konstruktora obiektu mechanicznego metody te mają niewielką wartość, gdyż niezawod­ności elementów obiektu mechanicznego nie są na ogół znane a priori a jego struktura niezawodnościowa stanowi tylko nie­wielki fragment takiego modelu, który może być wykorzystany do badań niezawodności tego obiektu (p. rozdz. 4). Wspomniane metody uwzględniają więc możliwości oddziaływania na poziom niezawodności projektowanegoobiektu jedynie przez zmiany jego struktury niezawodnościowej. Możliwości te są jednak nieduże, gdyż struktury niezawodnościowe obiektów mechanicznych nie są zwykle skomplikowane. Metody te nie uwzględniają natomiast bardzo dużych możliwości oddziaływania na ten poziom przez zmiany wielu innych czynników, które charakteryzują konstruk­cję oraz przewidywany sposób eksploatacji i przewidywany spo­sób wykonania obiektu i jego elementów.

Wpływ fazy konstruowania na niezawodność przyszłego obiek­tu zaznacza się dodatkowo przez ustalane wówczas wymagania kierowane do faz wytwarzania i eksploatacji. Między innymi dla fazy eksploatacji opracowuje się projekt sposobu eksploatacji obiektu (instrukcja użytkowania i obsługi), w którym określa się sposób użytkowania, częstość i jakość odnów profilaktycz­nych, zasady konserwacji, zasady napraw poawaryjnych itd. W projekcie tym określa się też sposób kontroli stanu tech­nicznego (diagnozowania) obiektu w okresie eksploatacji w ce­lu zwiększenia skuteczności odnów profilaktycznych, uprzedza­jących powstawanie uszkodzeń, te i inne wymagania kierowane z fazy konstruowania do faz wytwarzania i eksploatacji ustala­ne są głównie na podstawie tradycji i doświadczenia projektowania i eksploatowania podobnych obiektów.

Wpływ działań w fazie wytwarzania na poziom niezawodności obiektu jest wieloraki. Po pierwsze – sfera wytwarzania jest dla konstruktora źródłem in­formacji o możliwościach technologicznych wykonania projektowanego obiektu i jego elementów. Po drugie – odstępstwo od po­ziomu niezawodności określonego w fazie projektowania jest tym mniejsze, im większy jest stopień zgodności wyników procesu wytwarzania z wymaganiami na­rzuconymi w projekcie technicznym obiektu, dotyczącymi jego własności geometrycznych, materiałowych (w tym stanu warstwy wierzchniej) i innych. Zachowanie w procesie wytwarzania wspomnianych wymagań jest możliwe dzięki istnieniu w fazie wy­twarzania kontroli tego procesu (kontroli surowców, poszcze­gólnych operacji technologicznych, montażu itd.). Po trzecie – na po­ziom niezawodności wytwarzanego obiektu duży wpływ mają rów­nież decyzje podejmowane w fazie wytwarzania dotyczące sposo­bów obróbki i montażu oraz przebiegu tych procesów technolo­gicznych. Wymagane bowiem przez konstruktora własności obiektu mogą być uzyskane w różny sposób.

Czynniki technologiczne, wpływające na niezawodność przy­szłego obiektu, są na ogół trudno mierzalne. Z tego powodu można osiągnąć dobre rezultaty w zakresie zapewniania odpo­wiedniej niezawodności w fazie wytwarzania, jeśli przestrzega się pewnych zasad dotyczących przygotowania i organizacji pro­cesu technologicznego.

Możliwości oddziaływania w fazach wytwarzania i eksploatacji na niezawodność obiektu są znacznie większe w tym przypad­ku gdy przepływy informacji o obiekcie między fazami kon­struowania, wytwarzania i eksploatacji są wielokierunkowe (rys.l).

rysunek

Rys.1. Obieg informacji o niezawodności

Naturalne, jednokierunkowe przepływy informacji, tzn. z fazy projektowania do faz wytwarzania i eksploatacji oraz z fazy wytwarzania do fazy eksploatacji (zawartych między in­nymi w projekcie obiektu, w instrukcjach użytkowania i obsłu­gi, w wykonywanym obiekcie) nie są wystarczające w dobrze zor­ganizowanym systemie budowie obiektu. Dużo lepsza sytuacja występuje wówczas, gdy informacje o obiekcie są przekazywane w kierunku przeciwnym, np. wtedy, gdy informacje o zachowaniu się obiektu podczas eksploatacji, o jego niezawodności, o przyczynach i skutkach niesprawności docierają z fazy eksploa­tacji do pozostałych faz. Takie doświadczenia wynikające z eksploatacji tych obiektów mogą być w tym przypadku przyczyną pewnych zmian sposobu eksploatacji (np. częstości odnów profi­laktycznych), procesu wytwarzania, a nawet rozwiązania kon­strukcyjnego (ulepszenia obiektu). Zmiany te wprowadzane są za pośrednictwem faz projektowania i wytwarzania. Mają one na celu zwiększenie efektywności eksploatowania obiektu, m.in. zbliżenie uzyskanego poziomu niezawodności do poziomu pożąda­nego.

Dzięki istnieniu tych sprzężeń zwrotnych w przepływach in­formacji o obiekcie między poszczególnymi fazami staje się również możliwe tworzenie coraz doskonalszych innych typów obiektów.

Omawiane przepływy informacji są przedstawione w sposób poglądowy na rys.1. W celu wyróżnienia działań należących do fazy konstruowania są one na tym rysunku obwiedzione linią ciągłą.

Obserwacja i analiza procesów wytwarzania i eksploatacji oraz zbieranie i przetwarzanie wspomnianych informacji powinno być działaniem należącym do systemu konstruowania, co w spo­sób umowny zaznaczono również na rys.1. Tylko w takim przypad­ku można zapewnić dużą efektywność tych informacji.

Można też stwierdzić, że największe możliwości oddziaływa­nia na niezawodność obiektu istnieją w fazie jego projektowania. Prócz tego kształtowanie poziomu nieza­wodności w tej fazie może być najbardziej efektywne. Oznacza to, że do osiągnięcia zamierzonego poziomu niezawodności po­trzeba w tej fazie na ogół zdecydowanie mniejszych nakładów niż w przypadku, gdy poziom ten jest osiągany w wyniku dodat­kowych, nie przewidzianych w okresie projektowania działań w pozostałych fazach.

W praktyce jednak możliwości racjonalnego oddziaływania, z zamierzonym efektem, na poziom niezawodności w fazie projektowania są małe. Jak już wspomniano, jedną z zasadniczych przyczyn tego jest brak metod, a więc narzędzia, za pomocą którego konstruktor mógłby przeprowadzać teoretyczne badania niezawodności tworzonego przez siebie obiektu i poszukiwać najlepszych sposobów oddziaływania na poziom niezawodności te­go obiektu.