podrozdział pracy dyplomowej
Przyjmuje się wg pracy [24], że nominalny model niezawodnościowy jest to układ przedstawiony za pomocą opisu słownego i zwykle także graficznego, odwzorowujący w sposób uproszczony te stany i procesy charakterystyczne dla obiektu rzeczywistego oraz jego otoczenia, które są istotne z punktu widzenia niezawodności.
Budowa tej postaci modelu może się odbywać w czterech krokach, w których dokonuje się wyboru czynników charakteryzujących eksploatację obiektu; zjawisk fizycznych, które mogą prowadzić do niesprawności; punktów kontrolnych i struktury niezawodnościowej obiektu. Zasady tych działań są przedstawione poniżej.
Pierwszy krok, od którego rozpoczyna się w ogólnym przypadku budowy takiego modelu, to wybór i opis (głównie słowny) czynników Za(t), Ot (t) i U(t) charakteryzujących proces eksploatacji modelowanego obiektu. Celem czego działania jest ułatwienie rozpoznania i wyboru zjawisk fizycznych (w drugim kroku tworzenia modelu nominalnego) przebiegających w obiekcie w czasie eksploatacji i pogarszających jego stan techniczny. Grupy czynników Za(t), Ot(t) i U(t) zostały już przedstawiony w rozdz. 3. Tu dodajmy kilka wyjaśnień, które mogą ułatwić wybór innych czynników.
Elementy określające zadanie Za(t) są charakterystyczne dla modelowanego obiektu. Ich rodzaje zależą od celu, dla którego obiekt jest konstruowany. Dla różnych maszyn są więc one różne.
W ogólnym przypadku elementami stanu otoczenia obiektu Ot(t) są określone cechy warunków klimatycznych, warunków meteorologicznych, warunków lokalnych (np. agresywność chemiczna środowiska, zapylenie i zapiaszczenie powietrza, ukształtowanie terenu) itd. Wybór tych cech zależy jednak od rodzaju obiektu. Dla jednego obiektu istotnym elementem stanu otoczenia może być np. temperatura powietrza, a dla innego – prędkość wiatru.
Do pewnego stopnia opis czynników zaliczanych do sposobu eksploatacji U(t) może być niezależny od rodzaju modelowanego obiektu. W ogólnym przypadku czynniki te dzielą się na dwie grupy czynników charakteryzujących:
- użytkowanie
- obsługiwanie.
Elementy określające sposób użytkowania można podzielić na grupę elementów związanych z przebiegiem procesu użytkowania i na grupę elementów związanych z jakością użytkowania (np. sterowania). Te pierwsze to kolejność, liczby i czasy trwania różnych stanów użytkowania. Na przykład w przypadku żurawia samojezdnego sekwencję różnych stanów użytkowania mogą tworzyć następujące stany: dojazd do miejsca pracy, przygotowanie żurawia do wykonywania zadania, stany naprowadzania haka nad ładunek (sekwencja kilku następujących po sobie ruchów wysięgnika i haka lub ich skojarzeń, stany naprowadzania ładunku nad miejsce posadowienia wysięgnika i haka lub ich skojarzeń), posadowienie ładunku, stany naprowadzania haka nad nowy ładunek, … itd. Elementy związane z jakością użytkowania to: błędy użytkowania, płynność ruchów itd. W przypadku żurawia. samojezdnego takimi błędami użytkowania są m.in.: skośne ciągnięcie ładunku, podrywanie ładunku, niedostateczne wypoziomowanie żurawia, uderzenia o przeszkody itd. Jakość użytkowania zależy od: stopnia dopasowania zespołu cech psychofizycznych użytkownika (np. operatora) do obiektu, stopnia fachowości użytkownika itd. Czym niższa jakość użytkowania, tym jest większe prawdopodobieństwo pojawienia się stanów użytkowania niezgodnych z instrukcją użytkowania zabronionych, nieumiejętnego sterowania. Niska jakość użytkowania może więc być przyczyną pojawienia się szczególnie silnych oddziaływań zewnętrznych lub długiego trwania tych oddziaływań.
Elementy sposobu obsługiwania również można podzielić na grupę elementów związanych z przebiegiem procesu obsługiwania i na grupę elementów związanych z jakością obsługiwania. Pierwsze z nich to okresy między różnymi stanami obsługiwania i czasy trwania tych stanów. Wszystkie stany obsługiwania można podzielić na trzy zbiory stanów: diagnozowania technicznego (przeglądów), odnawiania profilaktycznego i odnawiania poawaryjnego (wymian, napraw, regulacji, smarowań). Również na jakość obsługiwania składają się: jakość przeglądów, jakość odnawiania profilaktycznego i jakość odnawiania poawaryjnego. Elementy związane z jakością obsługiwania to głównie wykrywalność nieodpowiedniego stanu technicznego podczas przeglądu oraz stopień poprawy stanu technicznego w wyniku odnowy. Czym niższa jest jakość przeglądów, tym mniejsza jest szansa wykrycia nieodpowiedniego stanu technicznego obiektu, a czym niższa jakość odnawiania, tym większa jest możliwość niepoprawienia tego stanu (bo na przykład odnowy nie przeprowadzono wcale), a nawet jego pogorszenia wskutek na przykład złego smarowania, złej regulacji, zastosowania niewłaściwego naciągu wstępnego itd.
W wielu publikacjach, podkreśla się, że jedną z głównych przyczyn niesprawności obiektów technicznych jest zła eksploatacja, głównie niezgodna z instrukcjami użytkowania i obsługiwania. Wskazuje to, jak ważny jest przy tworzeniu modelu niezawodnościowego umiejętny opis elementów sposobu eksploatacji U(t), głównie jakości użytkowania i jakości obsługiwania.
W pewnym stopniu wybór i opis cech charakteryzujących proces eksploatacji, dokonany w pierwszym kroku tworzenia modelu nominalnego, może być wykorzystany w etapie tworzenia niezawodnościowego modelu matematycznego głównie do matematycznego opisu procesu eksploatacji oraz zewnętrznych oddziaływań na obiekt.
Należy zaznaczyć, że w niektórych przypadkach ten pierwszy krok w tworzeniu modelu nominalnego może być pominięty całkowicie lub częściowo. Zachodzi to na przykład wtedy, gdy znane są rodzaje i poziomy oddziaływań zewnętrznych (np. w postaci histogramów obciążeń uzyskanych w wyniku eksploatacyjnych badań obiektów podobnych). Wówczas te właśnie znane oddziaływania stanowią podstawę wspomnianej identyfikacji i wyboru zjawisk fizycznych.
Drugim krokiem w procesie tworzenia modelu nominalnego jest wybór decydujących zjawisk fizycznych, pod wpływem których ulegają zmianom w czasie eksploatacji (zwykle niekorzystnym) różne własności obiektu, m.in. własności geometryczne i materiałowe decydujące o jego prawidłowym funkcjonowaniu, czyli jego stan techniczny (p. rozdz. 3). Przyczyną pojawienia się tych zjawisk są oddziaływania zewnętrzne występujące w czasie eksploatacji obiektu. W przypadku obiektu mechanicznego tymi zjawiskami fizycznymi są przede wszystkim: zmęczenie objętościowe i powierzchniowo elementów, rozwarstwienie doraźne materiału, zużycie cierne, pełzanie, korozja, plastyczne odkształcenie, zespół zjawisk typu rozregulowania, starzenie materiałów itd. Zjawiska te mogą zachodzić nie tylko w elementach mechanicznych, lecz również w elementach układów elektrycznych lub elektronicznych i prowadzić do niekorzystnych zmian charakterystyk elementów lub całych układów, a nawet przerwania obwodów elektrycznych. W rezultacie degradacji stanu technicznego pod wpływem tych zjawisk mogą w czasie eksploatacji obiektu pojawiać się jego niesprawności. Charakter tych zjawisk fizycznych jest bardzo złożony. Na ogół istnieją tylko hipotetyczne wyjaśnienia istoty tych zjawisk. Badaniem ich zajmuje się tzw. fizyka uszkodzeń.
Ze zbioru tych zjawisk należy przy budowie modelu wybrać głównie te, które przebiegają w obiekcie w sposób najbardziej intensywny i które mogą prowadzić do niesprawności powodujących duże straty (ekonomiczne i inne). W celu ułatwienia wyboru tych najbardziej istotnych zjawisk fizycznych, zachodzących w elementach mechanicznych, należy m.in.: przeprowadzić szacunkową analizę poziomów naprężeń mechanicznych w elementach obiektu, przeprowadzić analizę charakteru tych naprężeń (stałe, zmienne), określić czas ich występowania, poznać własności materiałów elementów, poznać czynniki otoczenia i intensywności ich oddziaływania Itd. Wyboru zjawisk fizycznych decydujących o niesprawnościach elementów układów elektrycznych i elektronicznych, które czasami są Integralną częścią obiektów mechanicznych, należy dokonywać według nieco innych zasad. Wynikają one z metod obliczeń, przeprowadzanych przez konstruktorów takich układów i zawarte są w odpowiednim piśmiennictwie, np. w [10].
Duży wpływ na trafność tego wyboru może mieć również analiza przyczyn niesprawności w eksploatowanych już podobnych obiektach mechanicznych, pracujących w podobnych warunkach oraz analiza przyczyn niesprawności, które wystąpiły podczas eksperymentalnych badań prototypów i serii informacyjnej.
Jednocześnie z wyborem decydujących zjawisk fizycznych dokonuje się jednego z podstawowych założeń upraszczających, polegającego na pominięciu innych zjawisk, które mają mały wpływ na proces powstawania niesprawności obiektu.
Trzeci krok to wybór fragmentów obiektu najbardziej narażonych na niesprawności, czyli wybór PK (p. rozdz. 4.1). Przyjmuje się przy tym następne bardzo ważne założenie upraszczające, według którego prawdopodobieństwo powstania uszkodzenia w innych miejscach jest równe zeru. Ciągłe modele niezawodnościowe obiektów mechanicznych stosowane są bardzo rzadko, gdyż są zbyt skomplikowane i zbyt trudne do badania.
Wyznaczanie PK może się odbywać różnymi sposobami w zależności od stopnia skomplikowania obiektu, od ważności spełnianych przez niego funkcji, od zasobu informacji o konstruowanym obiekcie i o eksploatowanych obiektach podobnych, od rodzajów metod obliczeń przeprowadzanych przez konstruktora itd. Są one następujące.
– Arbitralne wskazanie PK na podstawie wiedzy, doświadczenia i intuicji osoby tworzącej model obiektu. Jest to sposób najprostszy, lecz zwykle najmniej dokładny.
– Wskazanie PK na podstawie rezultatów obliczeń (m.in. naprężeń) przeprowadzonych przez konstruktora w etapach tworzenia projektu wstępnego i projektu technicznego oraz na podstawie rozważań przeprowadzonych w drugim kroku tworzenia niezawodnościowego modelu nominalnego.
– Wskazanie PK na podstawie informacji o niesprawnościach podobnych obiektów mechanicznych eksploatowanych w warunkach podobnych do tych, które są przewidziane dla obiektu rozpatrywanego.
– Wskazanie PK na podstawie rezultatów doświadczalnych badań elementów lub podzespołów konstruowanego obiektu, przeprowadzanych w etapach tworzenia projektu wstępnego i projektu technicznego oraz podczas badań prototypów (wizualne efekty badań elastooptycznych, akustyczne efekty dekohezji itd.).
– Wyznaczanie PK na podstawie rezultatów obliczeń metodą elementów skończonych, przeprowadzonych przez konstruktora w etapach tworzenia projektu wstępnego i projektu technicznego. W tym przypadku wyznaczanie PK może być zautomatyzowane dzięki dołączeniu do programu MES odpowiedniej procedury, służącej do wskazywania tych fragmentów obiektu, w których występują największe wytężenia (mechaniczne, cieplne i inne).
Niektóre z tych sposobów mogą być również wykorzystywane do wyznaczania takich PK, które zastępują pod wybranym względem grupy elementów obiektu ( p. rozdz. 4.1). Dotyczy to również tych przypadków, gdy w modelowanym obiekcie występuje duża grupa elementów o dużej niezawodności. Wówczas jednym ze sposobów postępowania może być przypisanie takiej grupie elementów jednej lub kilku wspólnych cech zdatności i traktowanie jej jako jednego PK.
Jeśli liczba PK, wyznaczonych tymi sposobami, jest duża, to można próbować ją ograniczyć przez eliminację niektórych z nich. Aby taka eliminacja była racjonalna, należy uprzednio dokonać hierarchizacji wszystkich PK. Do tego konieczne jest ustalenie kryterium, na podstawie którego można tę hierarchizację przeprowadzić. Wydaje się, że jedną z bardziej odpowiednich wielkości, która może w tym przypadku spełniać rolę wielkości kryterialnej, są straty wywoływane ewentualnymi niesprawnościami poszczególnych PK (straty ekonomiczne i inne). Wielkość ta jest zdefiniowana i opisana w opracowaniu [25]. Eliminacja powinna dotyczyć tych z wyznaczonych uprzednio PK, dla których wspomniane straty są według szacunkowej oceny najmniejsze.
Czwartym krokiem wyróżnionym w procesie budowy modelu nominalnego jest określenie zasad organizacji zbioru wybranych PK, czyli – wybór tzw. struktury nie zawodnościowej obiektu. W tym celu należy przede wszystkim podać definicje opisowe (słowne) niesprawności poszczególnych PK i całego obiektu, czyli określić ich graniczne stany techniczne, oddzielające odpowiednie stany zdatności i niezdatności,
Niesprawności PK obiektów mechanicznych przenoszących napęd charakteryzują się zwykle granicznym naruszeniem makro- lub mikrogeometrii elementów. Naruszenie makrogeometrii polega na: odkształceniach trwałych (wskutek: utraty stateczności, pełzania, przekroczenia przez obciążenia nośności granicznej itd.), ubytkach materiału (wskutek: zużycia ciernego, korozji itd.), pęknięciach (wskutek: przekroczenia przez obciążenie nośności granicznej, kumulacji uszkodzeń zmęczeniowych przy zmiennych obciążeniach itd.), przemieszczeniach w stosunku do sąsiednich elementów (wskutek utraty sprzężenia ciernego) itd. Naruszenie mikrogeometrii to zwykle: wgniecenia, wżery, wykruszenia i inne na powierzchni elementu (wskutek: adhezji, korozji, pittingu itd.).
Ogólnie opisowa definicja niesprawności PK może brzmieć na przykład w sposób następujący: niesprawność PK jest to takie zdarzenie (polegające zwykle na naruszeniu makro- lub mikrogeometrii elementu w tym PK), które uniemożliwia dalsze spełnianie przez ten PK wymaganych funkcji w obiekcie w sposób fizyczny lub umowny.
W każdym konkretnym przypadku PK należy taką definicję uściślić, zwłaszcza gdy ewentualna niesprawność jest umowna, przez ustalenie objawów granicznego stopnia naruszenia geometrii elementu. Jak wynika z ogólnej definicji niesprawności podanej powyżej o położeniu tej granicy mogą decydować różne kryteria, nie tylko techniczne.
Następnie należy ustalić definicję opisową niesprawności całego obiektu. Ogólnie może być ona sformułowana podobnie jak dla PK:
Def. [24] Niesprawność obiektu jest to każde zdarzenie, polegające na takiej zmianie stanu-technicznego tego obiektu, że uniemożliwia to fizycznie lub umownie spełnianie’ przewidzianych dla niego funkcji.
I tu także uściślenie tej definicji w odniesieniu do konkretnego obiektu powinno polegać na ustaleniu kryteriów niesprawności, czyli objawów granicznego pogorszenia stanu technicznego.
Zgodnie z zaproponowanymi definicjami obiekt i jego PK mogą ulegać niesprawnościom fizycznym lub umownym. Niesprawnościami fizycznymi nazwane zostały te, które natychmiast po ich zajściu uniemożliwiają w ogóle jakiekolwiek funkcjonowanie obiektu lub PK Są to głównie niesprawności występujące nagle, np.: pęknięcia i trwałe odkształcenia elementów mechanicznych lub większych fragmentów maszyny, pęknięcia przewodów doprowadzających olej do instalacji hydraulicznych, przerwanie istotnych obwodów elektrycznych itd.
Niesprawnościami umownymi nazywa się takie zmiany stanu technicznego obiektu (lub PK), zachodzące na ogół stopniowo, a czasami nagle, które nie przerywają natychmiast jego funkcjonowania, a jedynie wywołują:
– niedopuszczalny wzrost ryzyka powstawania poważnego uszkodzenia, powodującego duże straty (np. niesprawność układu zabezpieczenia w obiekcie, pojawienie się dużych drgań wskutek wzrostu luzu w łożyskach itd.);
– niedopuszczalne pogorszenie poprawności funkcjonowania obiektu, np. spadek wydajności, spadek sprawności mechanicznej, wzrost poziomu hałasu itd.
Ustalenie kryteriów niesprawności (fizycznych i umownych) zależy: od rodzaju funkcji przewidzianych do wykonania przez obiekt (lub przez maszynę zawierającą ten obiekt), od sposobu eksploatacji, a przede wszystkim od możliwości powstania dużych strat ekonomicznych lub możliwości zagrożenia dla życia ludzkiego w przypadku powstania niesprawności fizycznej obiektu. Czym te skutki ewentualnej niesprawności fizycznej są większe, tym kryterium niesprawności umownej ustala się na ogół na niższym poziomie.
Przyjęcie opisowych definicji niesprawności obiektu i poszczególnych jego PK jest podstawą do zorganizowania zbioru wybranych PK, czyli ustalenia struktury niezawodnościowej obiektu. Struktura niezawodnościowa obiektu określa zależność jego stanu niezawodnościowego (stan zdatności, stan niezdatności) od stanów niezawodnościowych poszczególnych jego PK.
Wśród struktur niezawodnościowych wyróżnia się, jak wiadomo, dwie podstawowe grupy struktur: struktury szeregowe i struktury równoległe. Obiekty mechaniczne przenoszące napęd mają zwykle strukturę szeregową w sensie niezawodności, czasami – strukturę mieszaną lub inną.
Trzeba jednak pamiętać, że struktura niezawodnościowa obiektu jest względna. Ten sam obiekt może mieć w pewnych przypadkach strukturę równoległą, a w innych – szeregową lub mieszaną. Zależy to głównie od definicji niesprawności obiektu. Na przykład inną strukturę niezawodnościową może mieć obiekt przy definicji niesprawności podanej powyżej, uwzględniającej fizyczny i umowny brak możliwości wykonania zadania, a inną – przy definicji uwzględniającej tylko fizyczny brak możliwości wykonania zadania. Przedstawmy prosty przykład zależności tej struktury od kryterium niesprawności.
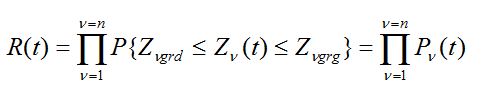 (44)
(44)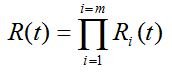 (45)
(45)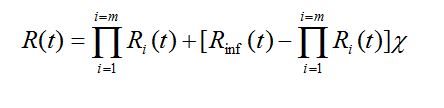
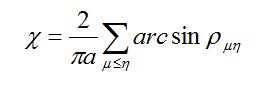
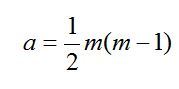 (47)
(47)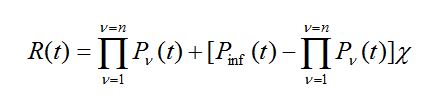 (48)
(48)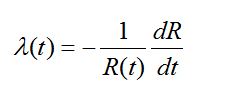 (49)
(49)