[z pracy magisterskiej]
W niniejszym rozdziale przedstawiono sposób przeprowadzania obliczeń niezawodnościowych w fazie projektowania urządzeń technicznych wg metody projektowania LEMACH 2 [8], ze względu na podatność jej struktury na rozgałęzienia algorytmów.
Wybór rodzaju obliczeń niezawodności, których należy dokonać na kilku etapach projektowania, uzależniony jest od fazy przybliżenia projektowego (tabela. 1).
Ze względu na podobieństwo toku obliczeń odpowiadających poszczególnym etapom projektowania, podjęto próbę algorytmizacji działań prowadzących do oceny niezawodności urządzenia.
Proponowany algorytm ma charakter ogólny i może być wykorzystany w innych metodach projektowania.
Sposób przeprowadzenia obliczeń niezawodnościowych wg zaproponowanego algorytmu przedstawiono na przykładzie orientacyjnej oceny niezawodności projektu wstępnego (etap III wg tab. 1) obrotowej wiertarki elektrycznej.
Algorytm oceny niezawodności projektowanych urządzeń technicznych:
- Dokonaj podziału projektowanego urządzenia na elementy. Podział przeprowadź w stopniu szczególności zależnym od fazy przybliżenia projektowego.
- Zidentyfikuj strukturę niezawodnościową urządzenia przy zastosowaniu jednej z podanych metod:
a) diagnostyki technicznej i zasad budowy testów rozpoznających stan niezawodności,
b) symulacyjnej,
i określ wzorem niezawodność strukturalną urządzenia.
Przy małym stopniu skomplikowania urządzenia identyfikacja nie wymaga stosowania wymienionych metod.
Zależność rodzaju obliczeń niezawodnościowych od etapu projektowania
(tabeli 1)
| Etap projektowania | Czynności projektowe
wg. metody „LEMACH 2” |
Rodzaj obliczeń niezawodnościowych |
| I | Rozpoznawanie potrzeb,
formułowanie problemu |
|
| II | Tworzenie i wybór koncepcji rozwiązania projektowego | Określenie wymagań niezawodnościowych dla projektowanego urządzenia np. w postaci prawdopodobieństwa poprawnej pracy, lub średniego czasu poprawnej pracy.
Szacowanie wskaźników niezawodnościowych dla n koncepcji urządzenie ( przy wyborze koncepcji optymalnej należy uwzględnić kryterium niezawodności) |
| II | Opracowanie syntezy, projekt wstępny | Orientacyjne obliczenie niezawodności (nie ma jeszcze pełnych informacji o parametrach i warunkach pracy poszczególnych elementów urządzenia, znana jest struktura tj. liczba elementów i współzależności między nimi) |
| IV | Opracowanie rozwiązania szczegółowego i ocena rozwiązania | Dokładne obliczenia niezawodności z uwzględnieniem warunków pracy i dodatkowych czynników zależnych od przyjętych szczegółowych rozwiązań konstrukcyjnych |
| V | Realizacja próbna projektu.
Badania, opracowanie wniosków, danych technologicznych i eksploatacyjnych |
Eksperymentalna ocena niezawodności.
Wykrycie elementów o niedostatecznej niezawodności, wprowadzenie odpowiednich korekt w końcowe obliczenia i koniecznych zmian konstrukcyjnych |
- Zbierz informacje niezawodnościowe o elementach:
a) z literatury, katalogów, norm – o postaciach i, parametrach rozkładów funkcji niezawodności, wyodrębnionych elementów urządzenia,
b) z banku informacji – o uszkodzeniach elementów urządzenia (o postaciach uszkodzeń, o średnich czasach pracy bezawaryjnej itp.)
c) w przypadku braku danych o uszkodzeniach wyodrębnionych elementów urządzenia – przyjmij dane niezawodnościowe elementów o podobnej konstrukcji, technologii i zastosowaniu, lub – wykorzystaj posiadane informacje niezawodnościowe o elementach wyższego, względnie niższego rzędu w stosunku do wyodrębnionych, lub – zleć przeprowadzenie niezawodnościowych badań konstrukcyjnych wyodrębnionych elementów urządzenia
UWAGA:
Jeżeli w kroku 3 algorytmu postąpiłeś zgodnie z 3a, pomiń kroki 4, 5 i 6.
- Wyznacz modele matematyczne rzeczywistych rozkładów uszkodzeń elementów, stosując
- metodę analizy statystycznej, lub
- metodę graficzną.
Wykorzystaj fakt, że najczęściej występującymi rozkładami czasu poprawnej pracy są rozkłady: wykładniczy, normalny, logarytmo-normalny, Weibulla.
- Wyznacz parametry otrzymanego rozkładu korzystając z:
- metody najmniejszych kwadratów,
- metody największej wiarygodności, lub
- tablic siatki prawdopodobieństwa rozkładu.
- Zweryfikuj przyjęte modele matematyczne rzeczywistych rozkładów uszkodzeń elementów przy pomocy wybranego testu zgodności: Kołmogorowa, Pearsona, Hartley’a, c – kwadrat.
- Oblicz wartości funkcji niezawodności poszczególnych elementów urządzenia. Wyniki obliczeń zestaw w tabeli oraz przedstaw graficznie przebiegi funkcji niezawodności.
- Oblicz niezawodność strukturalną projektowanego urządzenia.
UWAGA:
Krok 8 kończy ocenę niezawodności dla etapów II i III projektowania urządzenia wg metody LEMACH 2.
- Przeprowadź ocenę wyników szacowania niezawodności oraz ich i interpretację przy pomocy analizy wariancji, analizy regresji lub analizy spektralnej.
- W oparciu o uzyskane wskaźniki niezawodnościowe zaakceptuj projekt urządzenia lub ustal przesłanki do jego modyfikacji.
UWAGA:
Jeżeli do oceny niezawodności wybrałeś metody symulacyjne, dokonaj optymalizacji urządzenia wg kryteriów niezawodności.
Orientacyjna ocena niezawodności urządzenia na etapie III projektowania wg metody Lemach 2:
Wstępne określenie niezawodności projektowanego urządzenia przeprowadza się przy pomocy przybliżonych obliczeń, opartych na następujących założeniach:
- uszkodzenia elementów są zdarzeniami losowymi, wzajemnie niezależnymi,
- rozpatrywane są jedynie elementy wchodzące w skład zasadniczego układu funkcjonalnego,
- warunki pracy nie mają wpływu na niezawodność urządzenia.
Szacowanie niezawodności wg zaproponowanego algorytmu przeprowadzono dla szlifierki kątowej.
- Podział projektowanego urządzenia na elementy przedstawiono na rysunku 1.
1 – silnik,
2 – reduktor,
3 – sprzegło,
4 – przekładnia ślimakowa,
5 – bęben,
6 – lina.
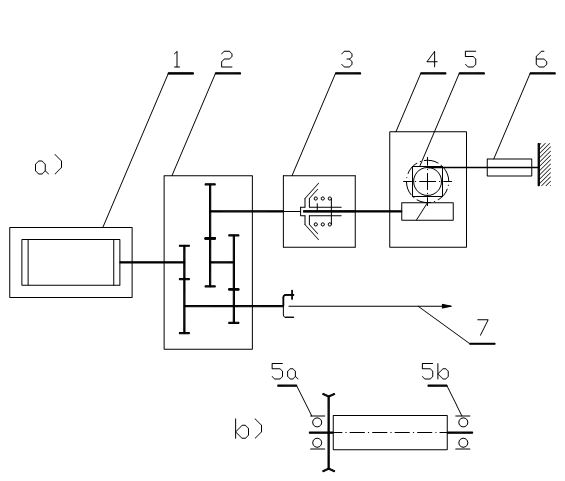 Rys. 9. Obrotowa wiertarka elektryczna do pracy z podpory z posuwowym mechanizmem kołowrotowym:
Rys. 9. Obrotowa wiertarka elektryczna do pracy z podpory z posuwowym mechanizmem kołowrotowym:
- schemat kinematyczny, b) sposób łożyskowania bębna:
1 – silnik, 2 – reduktor, 3 – sprzęgło, 4 – przekładnia ślimakowa, 5 – bęben,
5a, 5b – łożyska bębna, 6 – lina, 7 – wiertło
- Identyfikacja struktury niezawodnościowej urządzenia oraz określenie niezawodności strukturalnej.
Wiertarka posiada szeregową strukturę niezawodnościową, którą przedstawiono na rysunku 10.

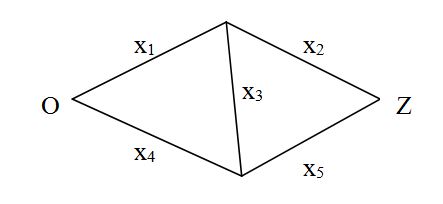
 (9)
(9)