Matematyczny model niezawodnościowy jest to zbiór relacji matematycznych i występujących w nich wielkości, opisujący te stany oraz procesy decydujące o niesprawnościach obiektu rzeczywistego, które są uwzględnione przez model nominalny. Sposób tego matematycznego opisu powinien być taki, aby nadawał się do określenia poziomu niezawodności badanego obiektu, a ściślej – do wyznaczenia wybranych wskaźników niezawodności.
Do budowy modelu matematycznego przystępuje się po zgromadzeniu dalszych informacji o obiekcie, potrzebnych w tym etapie modelowania (p. rozdz. 4.1). Wiele innych informacji gromadzi się również w trakcie tworzenia modelu matematycznego, gdyż wówczas precyzują się dalsze potrzeby w tym zakresie.
Tworzenie modelu matematycznego rozpoczyna się od podjęcia kilku wstępnych, ale istotnych decyzji, od których w dużym stopniu zależy postać matematyczna modelu niezawodnościowego [19]. Dotyczą one wyboru cech zdatności obiektu, jego miar niezawodności oraz metody przyszłych badań, przeprowadzanych na tworzonym modelu.
Należy po pierwsze dokonać wyboru cech zdatności badanego obiektu. Jak wynika z definicji tych wielkości, podanej w rozdziale 3, na wybór ich mają wpływ przede wszystkim rodzaje zjawisk fizycznych uwzględnionych przez model nominalny i możliwości łatwego zbudowania prostych relacji matematycznych, określających zależności tych cech od stanu technicznego i od poziomu oddziaływań zewnętrznych (p. zależność 4).
Po drugie należy dokonać wyboru najbardziej odpowiednich wskaźników służących do oceny niezawodności obiektu (np. funkcja niezawodności R, intensywność niesprawności l (wg PN – intensywność uszkodzeń [15], p. rozdz. 2), współczynnik gotowości Kg itd.). Od rodzaju wybranego wskaźnika niezawodności zależy w pewnym stopniu matematyczna postać tworzonego modelu niezawodnościowego, a także – jakość i ilość gromadzonych informacji o obiekcie i o jego eksploatacji. Spotykane w literaturze metody doboru wskaźników do oceny niezawodności konkretnych obiektów oparte są na ogół na ogólnej analizie charakterystyk konstrukcyjnych, sposobu eksploatacji, skutków niesprawności itd. oraz na intuicji. Te sposoby nie zaważę są zadowalające i mogą być przyczyną używania niepotrzebnych lub niewłaściwych wskaźników, niewiele mówiących o wpływie niezawodności obiektu na efektywność jego eksploatowania [25]. Znacznie lepszym sposobem jest dobieranie wskaźników niezawodności za pomocą odpowiednich szyfrów opracowanych na podstawie analizy wymienionych czynników.
Najbardziej właściwy dobór tych miar niezawodności powinien wynikać z potrzeb, a więc powinien być oparty na analizie matematycznego opisu kryterium globalnego służącego do oceny konstruowanego obiektu. Poziom niezawodności może być w najlepszym razie traktowany tylko jako kryterium cząstkowe oceny obiektu. Właściwie takim kryterium cząstkowym związanym z niezawodnością obiektu powinny być straty wywoływane niesprawnościami obiektu. Innymi kryteriami cząstkowymi, prócz tych strat, stosowanymi do oceny obiektu są na przykład takie cechy obiektu, jak: bezpieczeństwo, efektywność ekonomiczna, ciężar itd.
Kryteriami globalnymi ujmującymi takie różne cechy obiektu może być efektywność globalna lub tzw. dobroć obiektu [25]. Podstawą wyboru potrzebnych wskaźników niezawodności jest w tym przypadku matematyczny opis zależności takiego kryterium globalnego od wielkości wyrażających poziom niezawodności. Te właśnie wielkości powinny spełniać rolę wskaźników niezawodności.
Natomiast dobór wskaźników niezawodności dla PK obiektu złożonego wynika bezpośrednio ze sposobu wyrażenia niezawodności tego obiektu za pomocą niezawodności jego PK (p. dalsza część tekstu).
Po trzecie – określa się sposób wykorzystania niezawodnościowego modelu obiektu, tzn. określa się, czy będzie on służył do analitycznych czy numerycznych (symulacyjnych) badań niezawodności (p. rozdz. 5). W wielu przypadkach zależy od tego postać matematyczna modelu.
Po podjęciu tych przedstawionych powyżej decyzji przystępuje się do szczegółowego opisu matematycznego tych informacji, które zawarte są w modelu nominalnym. W efekcie tych działań otrzymuje się zbiór relacji matematycznych, które w sposób szczegółowy wyrażają to co relacje matematyczne (2) – (5) ogólnej postaci modelu matematycznego przedstawionego w rozdziale 3. W utworzonej w ten sposób szczegółowej postaci modelu matematycznego wyróżnić można kilka części odwzorowujących: a) początkowy stan techniczny obiektu, b) eksploatację systemu, w którego skład wchodzi badany obiekt; c) oddziaływania zewnętrzne na obiekt; d) oddziaływania wewnętrzne (między elementami); e) uogólnione wytężenia w poszczególnych PK; f) degradację stanu technicznego obiektu; g) granicę obszaru. zdatności obiektu.
Część a) przedstawia początkowy stan techniczny eO . Część b) opisuje w sposób szczegółowy czynniki Za , Ot i U (zadanie, stan otoczenia i sposób eksploatacji) przedstawione w rozdziale 3 przy prezentowaniu ogólnej postaci modelu. Część c) odpowiada relacji (2) ogólnie przedstawionej w rozdziale 3. Części d)- f) – to szczegółowe postacie relacji (3) i (4) z tego rozdziału. Część g) odpowiada relacji (5) z tego samego rozdziału.
Przedstawmy teraz krótko poszczególne części takiej szczegółowej postaci modelu matematycznego i opiszmy sposoby ich tworzenia.
a) Model początkowego stan technicznego obiektu jest to matematyczny opis stanu technicznego eO obiektu w chwili t = 0, ożyli początkowych własności geometrycznych, materiałowych i innych konstrukcyjnych (np. naciągów wstępnych), istotnych z punktu widzenia niezawodności (p. rozdz. 3). W przypadku konkretnego obiektu istotne są te własności, które mają wpływ na wielkości wybranych wcześniej cech zdatności l ich wartości granicznych. Jeśli największa liczba wielkości opisujących początkowy stan techniczny któregokolwiek PK wynosi r, a liczba PK wynosi m, to informacje o początkowych własnościach pojedynczego egzemplarza obiektu można zgrupować w postaci następującej macierzy
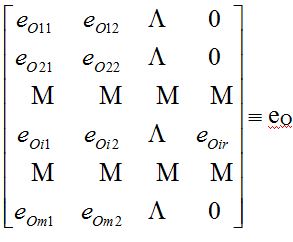 (9)
(9)
gdzie eOi1 , eOi2 ,…, eOir ,… są wielkościami określającymi początkowe własności i-tego PK. Zbiór wielkości opisujących początkowy stan techniczny obiektu można przedstawić również i w innej formie.
Dla populacji obiektów wielkości te mają mniejsze lub większe rozproszenia losowe. Są one nieuniknione jako skutek procesu wytwarzania. Wpływ tych rozproszeń na wartości cech zdatności w wielu przypadkach jest istotny. Wówczas wyrazy macierzy (9) są w ogólności realizacjami zmiennych losowych eOir . Jeśli wartość dystrybuanty FOir (eOir) zmiennej losowej eOir wynosi pOir, to odpowiedni wyraz macierzy (9) może być traktowany jako funkcja odwrotna do tej dystrybuanty, czyli
eOir= FOir-1 (pOir) (10)
Do określenia takich wielkości jest więc potrzebna znajomość matematycznej postaci ich rozkładów oraz wartości odpowiednich parametrów.
Początkowe własności materiałowe PK obiektu (wytrzymałość doraźna, wytrzymałość na zmęczenie, granica plastyczności itd.) zależą od wielu czynników (skład chemiczny, warunki wytopu, obróbka cieplna wlewków, technologia elementu, obróbka cieplna itd.), a wpływ na te własności każdego z nich nie jest dominujący. Dlatego rozkłady tych zmiennych losowych można zwykle aproksymować rozkładem normalnym (lub logarytmo-normalnym).
W wielu przypadkach również i początkowe własności geometryczne (promienie zaokrągleń w miejscach spiętrzenia naprężeń, luzy itd.) można zwykle aproksymować rozkładem normalnym.
Jeżeli w skład badanego obiektu wchodzą łożyska toczne, to model początkowego stanu technicznego powinien określać początkowe nośności ruchowe (lub trwałości) tych łożysk, nośność i trwałość łożyska można traktować jako zmienne losowe. Wyniki badań wskazują, że trwałość łożyska tocznego można aproksymować rozkładem Weibulla. W wymienionych pracach podane są matematyczne postacie rozkładów i wartości parametrów odpowiednich zmiennych losowych, określone na podstawie badań eksperymentalnych.
Jednak w wielu przypadkach brakuje danych potrzebnych do probabilistycznego lub statystycznego opisu początkowych własności obiektu. Wówczas można operować modelami hipotetycznymi, mniej dokładnymi, zbudowanymi na podstawie innych informacji, m.in. o matematycznych postaciach rozkładów podobnych wielkości, o okresach wartości niektórych wielkości, o wartościach tolerancji itd.
Te własności obiektu, których rozproszenia losowe mają nieistotny wpływ na cechy zdatności i ich wartości graniczne, przyjmuje się w celu uproszczenia modelu za wielkości zdeterminowane.
b) Model procesu eksploatacji jest to matematyczny opis cech charakteryzujących proces eksploatacji i uwzględnionych przez model nominalny (p. rozdz.2). W ogólnym przypadku jest to opis stochastyczny. Dane potrzebne do tego opisu mogą być opracowane na podstawie: badań eksploatacyjnych obiektów podobnych, na podstawie danych literaturowych, instrukcji użytkowania i obsługiwania obiektu badanego lub obiektów podobnych, na podstawie opinii ekspertów [12].
W ogólnym przypadku model procesu eksploatacji systemu, w którego skład wchodzi badany obiekt, to matematyczny opis poszczególnych elementów zadania Za , stanu otoczenia Ot i sposobu eksploatacji U (p. rozdz. 4.2).
Jeśli więc elementy zadania Za oznaczyć symbolami EZa1 , EZa2 ,…, EZaz gdzie z jest liczbą tych elementów, to w ogólnym przypadku opisem elementów zadania może być zbiór funkcji
FZa1(EZa1), FZa2(EZa2),…,FZaz(EZaz) (11)
FZai, jest tu symbolem odpowiedniej dystrybuanty lub częstości występowania.
Matematycznym opisem elementów EOt1 , EOt2 ,…, EOto stan otoczenia Ot może być zbiór dystrybuant lub częstości występowania tych elementów, czyli
FOt1(EOt1), FOt2(EOt2),…, FOto(EOto) (12)
Matematyczny opis elementów sposobu eksploatacji U zacznijmy od opisu przebiegu procesu użytkowania, czyli kolejności, liczb i czasów trwania różnych stanów użytkowania. Stan użytkowania maszyny jest to zbiór ruchów, jednocześnie przez nią wykonywanych, w sposób istotny różniący się ze względu na kinematykę, a zwłaszcza ze względu na zewnętrzne oddziaływania, od innych możliwych zbiorów ruchów (p. rozdz. 4.2).
[ciąg dalszy tej pracy nastąpi]