Używana powszechnie metodologia analizy niezawodności systemu oparta jest na teorii procesów Markowa. Ogólnie, proces wyznaczania niezawodności systemu za jej pomocą można podzielić na następujące etapy:
- określenie zbioru stanów niezawodnościowych,
- określenie macierzy przejść pomiędzy stanami,
- budowa odpowiedniego układu równań liniowych lub różniczkowych,
- rozwiązanie układu równań i wyliczenie na podstawie otrzymanych rozwiązań odpowiednich charakterystyk niezawodności systemu.
Taki sposób postępowania daje zadowalające wyniki w przypadku stosunkowo mało skomplikowanych systemów, dla których liczność przestrzeni stanów nie jest zbyt duża. W prostych przypadkach udaje się rozwiązać odpowiednie układy równań różniczkowych i możliwa jest wtedy nawet analiza obejmująca przypadek niestacjonarny. Jednak mając do czynienia z systemami bardziej skomplikowanymi szybko natrafia się na trudności powodowane nadmiernym wzrostem liczby stanów niezawodnościowych systemu, a co za tym idzie wzrostem liczby równań do rozwiązania. Istniejące prawda, czasem bardzo subtelne metody obliczeniowe, pozwalające na rozwiązywanie numeryczne nawet bardzo dużych układów równań. Jednak ich bezpośrednie wykorzystanie bez wcześniejszego przygotowania może okazać się często zbyt kłopotliwe.
Mimo tego nie wymiar zadania i trudności numeryczne przy jego rozwiązaniu są tutaj podstawowym problemem. W wielu przypadkach niezbędne w omawianym sposobie analizy założenie o wykładniczych rozkładach czasów przejść pomiędzy stanami może okazać się nie do przyjęcia. W praktyce bowiem analizujący system dysponuje a’priori pewną wiedzą na temat tych rozkładów. Wiedza ta pochodzić może na przykład z wcześniej wykonanych badań niezawodnościowych i w ewidentny sposób wskazywać, że pewne rozkłady wykładniczymi być nie mogą.
Zachodzi więc pytanie, co zrobić, gdy system jest stosunkowo skomplikowany i z założenia wiadomo, że niektóre rozkłady zmiennych losowych opisujących czasy przejścia pomiędzy stanami nie mogą w żadnym przypadku zostać uznane za rozkłady wykładnicze.
Można zaproponować wtedy poniższy sposób postępowania:
- określenie zbioru elementów systemu i ich stanów niezawodnościowych,
- sformalizowanie opisu stanu systemu za pomocą pewnych wyrażeń logicznych, których argumentami są stany niezawodnościowe elementów,
- określenie rozkładów czasów przejść pomiędzy stanami (mogą one być dowolne, byle tylko były znane),
- zastosowanie symulacji metodą Monte Carlo.
W metodzie istotne znaczenie ma sposób określenia stanu na podstawie stanów elementów. Proponuje się wykorzystanie opisu za pomocą tzw. funkcji struktury [6], która w formalny sposób odwzorowuje stany niezawodnościowe elementów systemu na stan niezawodnościowy systemu.
Dla lepszego wyjaśnienia wprowadzonych pojęć rozważmy system złożony z n elementów e1, e2,…, en oraz oznaczmy xi = l, gdy element jest e1 prawny oraz xi = O w przeciwnym przypadku. Jeśli y będzie zmienną stanu systemu, taką że y = l, gdy system jest sprawny i y = 0 dla systemu niesprawnego, wówczas odwzorowanie y = f( x1, x2,…, xn ) jest nazywane funkcją struktury systemu.
Przykładowo dla struktury szeregowej systemu funkcję struktury można zapisać jako:
y = x1´ x2´ … ´ xn
podobnie dla struktury równoległej zapis jest prosty:
y = l – (l –x1) ´ (l – x2) ´ … ´ (l – xn).
Dla przykładowej struktury mostkowej (rys. 3) funkcja struktury ma już bardziej skomplikowaną postać:
y = 1 – (1- x1x2) ´ (1- x4x5) ´ (1- x1x3x5) ´ (1- x2x3x4).
Krawędzie grafu przedstawionego na rys. 3. odpowiadają elementom systemu. System jest sprawny, gdy istnieje ścieżka od węzła C do Z, przy czym sprawność elementu oznacza, że odpowiadająca mu krawędź może występować w ścieżce (krawędź należy do grafu).
Dla systemów spotykanych w praktyce, gdzie ilość elementów może być znacznie większa niż w powyższym przykładzie, zaś struktura niezawodnościowa bardziej skomplikowana, zapisanie funkcji struktury w postaci analitycznej może być trudne.
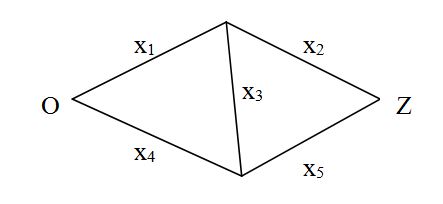
Rys. 4. System o strukturze mostkowej [6]
Również stabelaryzowanie tej funkcji może być mało realne wobec wystąpienia 2n możliwych wartości argumentów funkcji. Jednak warto zauważyć, że w celu wyznaczenia parametrów systemu metodą symulacyjną nie jest konieczna znajomość funkcji struktury w postaci analitycznej lub standaryzowanej;
wystarczy jedynie, że można podać procedurę, która określi wartość tej funkcji dla każdego zadanego wektora (x1, x2,…, xn).
W przypadku struktury mostkowej z rys. l procedura taka może być sformułowana następująco:
(i) dla zadanego wektora (x1,…, x5). zbudować graf (przez usunięcie krawędzi odpowiadających elementom uszkodzonym);
(ii) sprawdzić, czy istnieje ścieżka od węzła O do Z, jeśli lak, wówczas podstawić y = l (w przeciwnym przypadku y = 0).
Przykład jest stosunkowo prosty i postępowanie takie wydaje się niepotrzebną komplikacją, jednak w przypadkach skomplikowanych struktur spotykanych w praktyce może to być jedyny skuteczny sposób umożliwiający odwzorowanie stanów elementów na stan systemu, a dalej symulacyjne wyznaczenie parametrów niezawodnościowych systemu.
W porównaniu z metodą opartą na teorii procesów Markowa opisany wyżej sposób postępowania ma szereg cech pozytywnych. Po pierwsze istnieje w tym przypadku możliwość wyznaczenia dowolnych parametrów punktowych, na przykład współczynnika gotowości systemu, czy średniego czasu sprawności lub niesprawności. Po drugie, co jest być może bardziej istotne, istnieje możliwość estymacji rozkładów dowolnych czasów przebywania w stanie lub zbiorze stanów. Wyznaczenie rozkładów wymaga oczywiście właściwego przetworzenia wyników symulacji i zastosowania odpowiednich metod wnioskowania statystycznego. Podejście symulacyjne pozwala w końcu także na łatwiejszą analizę kosztów, na przykład kosztów napraw. Podobnie jak w przypadku czasów przebywania w stanach analiza taka jest możliwa nie tylko punktowo, ale również traktując odpowiedni koszt jako zmienną losową można estymować jego rozkład.
Symulacja metodą Monte Carlo ma więc szereg zalet. Wymaga jednak właściwego przygotowania danych, odpowiedniego oprogramowania, mocy obliczeniowych i czasu na wykonanie. Jednak za jej pomocą można analizować w zasadzie dowolne systemy przy dowolnych założeniach. Aspekt trudności obliczeniowych staje się coraz mniej istotny. Stosowane obecnie komputery są już tak wydajne, że nawet domowe urządzenia klasy PC mogą zostać wykorzystane do wykonywania bardzo złożonych obliczeń symulacyjnych w realnym czasie.