Można postawić pytanie, jakie są konieczne warunki, aby ciąg {P_k} był ciągiem rosnącym i jaka jest jego granica. Tak jak już było powiedziane k-ty wyraz ciągu przyjmuje postać

Wyraz P_k będzie większy od P_k-1, jeżeli

.                                                                                                 (62)

Zależność (62) podaje warunek na to, aby P_k > P_k-1 Gdy spełniona jest równość

,                                                                                                 (63)

to wyraz P_k  nie może być większy od P_k-1  Skoro tak, to warunek (63) powinien zapewnić, że ciąg (62) jest rosnący do wyrazu P_k. Stąd można wyciągnąć wniosek, że granica ciągu {P_k} jest następująca:

.                                                                                       (64)

Wartość prawdopodobieństwa, którą można uzyskać w pojedynczej próbie, jest uwarunkowana możliwościami naukowo-technicznymi. Jeżeli jest ciągły proces poprawiania konstrukcji ( a  > 0) oraz niedopuszczalna jest możliwość pogorszenia konstrukcji ( b = 0 ), to wówczas ciąg (61) zbieżny jest do jedności,

.                                                                                        (65)

Z zależności (65) wynika, że dla pewnego poziomu konstruowania i badania możliwy jest do osiągnięcia tytko pewien określony poziom niezawodności. Czyli po odpowiedniej liczbie cykli ( faz projektowania i badań ) powinien poziom niezawodności zbliżyć się do stanu równowagi.

Mając określone prawdopodobieństwo P_k można określić ciąg rozkładów dwumianowych dla próbki N – elementowej ( N modeli wyrobu k-tej wersji):

j = 1, 2,…, N,                                                                                                  (66)

k = 1, 2, 3,…

Dla każdego P_k otrzymuje się rozkład liczby sukcesów w próbce N- elemen­towej.

Jak już powiedziano, średnie wartości tych sukcesów będą wynosiły:

.                                                                                              (67)

Wariancje natomiast będą miały postać

.                                                                         (68)

Z postaci wzorów (67) i (68} wynika, że dla danej próbki N-elementowej, jeżeli P_k będą rosły, to średnie E_k[X_k^N] będą również rosły, a wariancje s_k² będą malały.

Dla ustalonego poziomu prac konstrukcyjnych i poziomu badań okreś­lonych przez a i b, ciąg rozkładów (66) (dla warunku (64)) będzie zbieżny do rozkładu:

,                                       (69)

j = 1,…, N.

Stąd możliwy do osiągnięcia rozkład ma postać następującą:

.                                                (70)

Wykorzystując (70) można określić prawdopodobieństwo, jakie możliwe jest do osiągnięcia dla przyjętego poziomu konstruowania i badań,

,                                                        (71)

gdzie j* jest wyznaczone z założeń na pojedynczą próbę. Schemat rozkładów dwumianowych dla kolejnych cykli badań pokazany jest na rys. 5.

Można również przedstawić zarys modelu kształtowania niezawodności wyrobu, gdy a i b przyjmują zmienne wartości w poszczególnych fazach projektowania i badań. Wzory na prawdopodobieństwa sukcesu lub porażki dla k-tej wersji modelu wyrobu przyjmują postać

,                                                                     (72)

gdzie P_k + q_k = 1.

Dla próbki N-elementowej rozkład dwumianowy przyjmuje postać

,                                                                           (73)

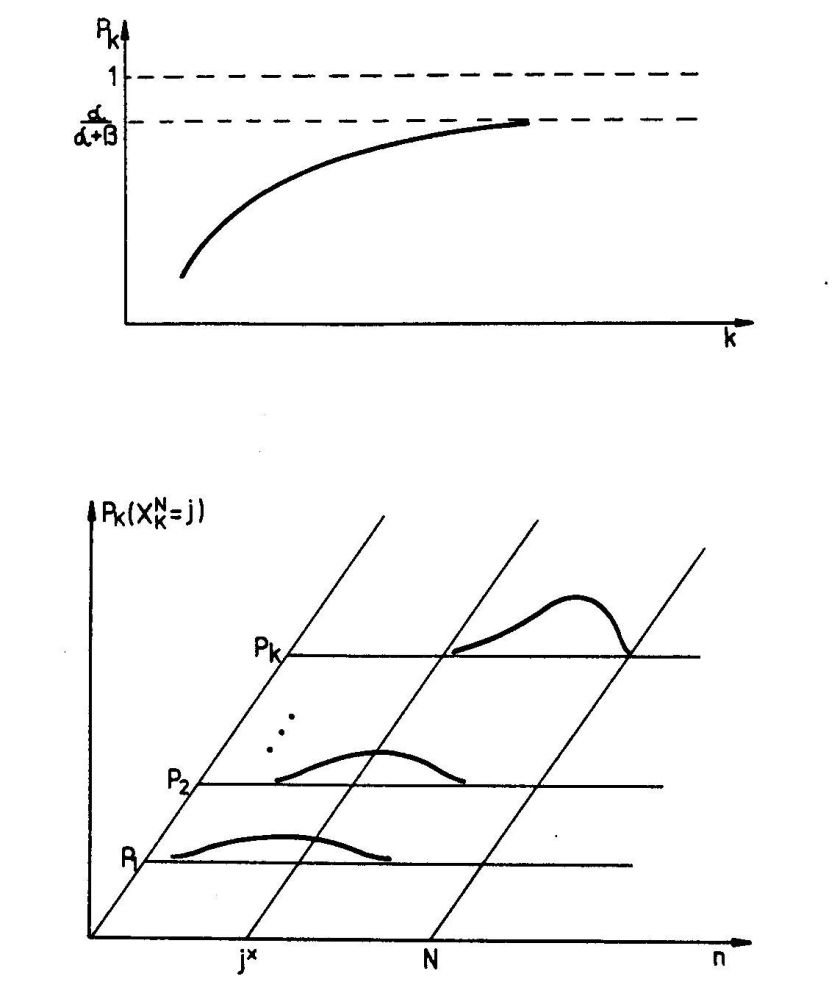
Rys. 7. Wykres P_k

Dla dolnej granicy prawdopodobieństwa niezawodnej pracy wyrobu wzór przyjmuje postać

,                                                                           (74)

gdzie j* wyznacza się w warunku P_k = j* /N ( j* — minimalna liczba sukcesów w próbce N-elementowej, P_k – dolna dopuszczalna granica prawdopodobień­stwa poprawnej pracy modelu).

W rezultacie projektowania i badań otrzymuje się następujący ciąg:

P₁, P₂, P₃,…, P_k, P_k+1,… = {P_k}                                                                        (75)

W procesie projektowania dąży się do tego, aby ten ciąg był rosnący.

Można postawić pytanie, jakie muszą być spełnione warunki, aby ciąg (75) był ciągiem rosnącym, uwzględniając, że w każdej fazie projektowania i badań  a_k i b_k zmieniają swoje wartości. Zgodnie z (72) k-ty wyraz ciągu określa się następującym wzorem:

Dokonuje się przekształcenia powyższego wzoru:

Oznacza  się    , Aby  P_k > P_k-1, to A > 0,

, ,                                         (76)

Aby P_k > P_k-1, to musi być spełniony warunek (76). Ponieważ prawa strona nierówności (76) zależy od właściwości cech projektowych w k-tej fa-zie projektowania i badań, to jeżeli

P_k-1 < a_k /( a_k + b_k ) otrzymamy P_k > P_k-1.

Skoro a_k i b_k zmieniają się w każdej fazie projektowania i badań, to możemy postawić pytanie, jak mają się zmieniać ciągi {a_k} i {b_k}, aby ciąg (75) był ciągiem rosnącym. W wyniku projektowania powinno się zapewnić:

.                                                                                 (77)

Dokonuje się przekształcenia zależności (77):

(78)

Warunek (78) można również napisać w następującej postaci:

.                                                                                                  (79)

Zależność (78) będzie zawsze spełniona, gdy (a) ciąg {a_k}  będzie rosnący;

(b) ciąg {b_k} będzie malejący. Jeżeli zależność (78) lub (79) będzie spełniona dla każdego k, to ciąg (75) będzie rosnący. Jeżeli te warunki będą spełnione, to w wyniku procesu projektowania otrzymamy, po odpowiedniej liczbie faz projektowania i badań, wyrób o żądanych cechach niezawodnościowych.

Omówiony przypadek jest w pewnym sensie uproszczeniem problemu. W praktyce projektowania powstają niekiedy rozwiązania nietrafne, które powodują obniżenie prawdopodobieństwa poprawnej pracy. W następnej fazie (w miarę rozpoznawania problemu) powstają pomysły bardziej udane, które wpływają na rozwiązania bardziej trafne, co w wyniku prowadzi do wzrostu prawdopodobieństwa poprawnej pracy. W wyniku całego procesu projek­towania w czasie mogą być przypadki, że ciąg (75) w pewnych przedziałach czasu jest ani rosnący, ani malejący. Dopiero po zdobyciu doświadczenia przekształca się w ciąg rosnący.

Rozpatrzone zostaną obecnie niektóre przypadki szczególne procesu kon­struowania i badań:

1. Niech a_k = 0, b_k = 0, k = 2, 3,…

Ze wzoru (72) wynika, że wszystkie wyrazy ciągu (75) przyjmują taką samą wartość. Cechy niezawodnościowe modeli wyrobu przy tym sposobie projek­towania pozostają takie same jak w etapie pierwszym-

2. a_k ¹ 0, b_k = 0, k = 2, 3,…

W tym przypadku mamy ciągły proces poprawiania konstrukcji. Ciąg (75) jest rosnący. Granicą ciągu jest l.

3. a_k = 0, b_k ¹ 0, k = 2, 3,…

W tym przypadku mamy ciągły proces pogarszania konstrukcji. Ciąg (75) jest malejący. Granicą ciągu jest 0.

4. a_k = 1, b_k = 1, k = 2, 3,…

Ze wzorów (72) wynika, że gdy a_k = 1 i b_k = 1 ( k = 2, 3,…, ), to w każdym kroku następuje zamiana P_k na q_k, a q_k na P_k. W praktyce oznacza to, że w każdej następnej fazie projektowania i badań poprawiamy wszystkie stany zawodne modeli wyrobu ( a_k = 1 ) i jednocześnie pogarszamy wszystkie stany niezawodne modeli wyrobu ( b_k = 1 ).

5. a_k ¹ 0, b_k ¹ 0 i a_k + b_k = 1

Dla lego przypadku wzory (72) przyjmują postać:

.                                                                    (80)

W tym przypadku a_k i b_k stają się prawdopodobieństwami pracy modeli w poszczególnych krokach. Oznacza to, że nie nakłada się historia projek­towania z poprzednich faz.

6. Niekiedy w pracach projektowo-badawczych chodzi nam o szybkie rozwiązanie problemu, bez względu na koszty. Wtedy proces projektowo-badawczy, zaproponowany wg schematu (rys. 5), można przyspieszyć.

W czasie Dt, w k-tej fazie projektowania, wykonuje się niejedną wersję modeli wyrobu a kilka różnych wersji modeli. Wtedy otrzymuje się ciąg wyników:

P_k1, P_k2,…, P_ki,

gdzie i oznacza liczbę wersji modeli w k-tej fazie projektowania.

Wyniki prawdopodobieństw P_ki poddaje się obróbce statystycznej, aby uwzględnić ewentualne różnice w liczności poszczególnych próbek oraz aby ustalić istotne bądź nieistotne różnice pomiędzy wynikami prawdopodobieństw.

Do następnej fazy projektowania (k + l), wybiera się tę wersję modelu, który w fazie k osiągnął najwyższą wartość prawdopodobieństwa P_ki. W przy­padku. gdy różnice P_ki dla różnych wersji modeli są nieistotne, o wyborze decydują inne czynniki (cechy), np. prostota konstrukcji.