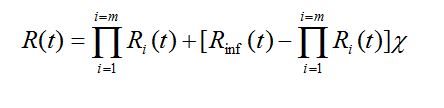Szczegółowa postać zależności, np. (l), wskaźnika niezawodności R od różnych czynników ck, ct i ce, otrzymywana w sposób analityczny, zależy głównie od rodzaju przyjętego wskaźnika niezawodności; rodzaju zjawisk fizycznych pogarszających stan techniczny obiektu, uwzględnionych w zbudowanym modelu; stopnia złożoności obiektu (przyjętej liczby PK) itd.
Najprostszy przypadek zachodzi wówczas, gdy badanym obiektem jest PK z jedną cechą zdatności Z (t). Wskaźnikiem służącym do oceny niezawodności PK jest zwykle funkcja niezawodności R(t), a inne na ogół jednoznacznie z niej wynikają. Jeśli granica obszaru zdatności jest jednostronna i określona przez Zgr , to wielkość R(t) może być wyznaczona na przykład na podstawie relacji
R(t) = P{ Z(t) £ Zgr } (40)
lub relacji
R(t) = P{T > t } (41)
Czas T bezawaryjnej pracy PK jest równy czasowi eksploatacji, jaki upływa do chwili tgr, w której cecha zdatności osiąga swoją wartość graniczną. Ponieważ wielkość tg,- wynika z relacji
Z(tgr) = Zgr (42)
do wyznaczenia funkcji niezawodności R(t) potrzebna jest znajomość stochastycznego opisu cechy zdatności Z(t). Opis ten wynika z niezawodnościowego modelu PK, a zwłaszcza jego części opisujących zmiany stanu technicznego i początkowy stan techniczny tego PK. Dla każdego PK i zjawisk fizycznych prowadzących do jego niesprawności opis ten może być więc różny.
Jeśli analiza cechy zdatności wskazuje, że jej dystrybuanta dla chwili t wynosi Fz(Z; t), to zgodnie ze związkiem (40) wielkość R(t) można określić na przykład za pomocą wyrażenia
R(t) = Fz(Zgr; t). (43)
W wielu przypadkach przy wyznaczaniu wskaźnika R(t) wystarczająca jest znajomość probabilistycznego opisu wielkości określających cechę zdatności.
Spośród analitycznych metod wyznaczania szczegółowej postaci relacji (1) dla PK o jednej cesze zdatności, należy wyróżnić małą grupę, rzadko używanych, metod opartych na teorii łańcuchów Markowa. Próby zastosowania tych metod przedstawione są w pracach [38,121]. W tych przypadkach niezawodnościowy model obiektu przygotowuje się w nieco odmiennej postaci matematycznej niż przedstawiona w rodz. 4, chociaż na niej opartej.
Gdy stan niezawodnościowy PK zależy od n cech zdatności, z założenia niezależnych stochastycznie (p. podrozdz. 5.1), to z formuły (6) wynika, że na przykład funkcja niezawodności tego PK jest równa
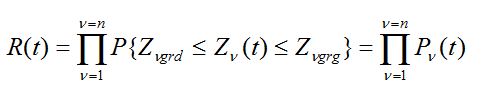 (44)
(44)
W tym przypadku analityczne wyznaczenie funkcji R (t) polega na wymnożeniu znalezionych uprzednio prawdopodobieństw tego, że w czasie t każda z n cech zdatności PK nie przekroczy granicy obszaru zdatności .
Przy takim samym upraszczającym założeniu niezależności stochastycznej en bloc między n cechami zdatności Zn(t) obiektu złożonego z m PK, a więc – również niezależności stochastycznej en bloc między m czasami Ti bezawaryjnej pracy PK, wskaźniki niezawodności takiego obiektu złożonego mogą być wyznaczone analitycznie na podstawie znajomości odpowiednich wskaźników niezawodności poszczególnych PK (lub nawet cech zdatności) oraz struktury niezawodnościowej obiektu. Jeśli na przykład poszukiwanym wskaźnikiem jest funkcja niezawodności a obiekt ma strukturę szeregową w sensie niezawodności (w odniesieniu do jego PK lub cech zdatności), to ten wskaźnik może być wyznaczony na podstawie formuły (44) lub formuły
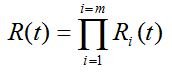 (45)
(45)
Przedtem należy jednak znaleźć odpowiednie prawdopodobieństwa Pn (44) lub funkcje Ri (45), do czego należy wykorzystać zbudowane modele niezawodnościowe PK.
Gdy niezawodnościowy model obiektu złożonego z większej niż 1 liczby PK lub niezawodnościowy model PK opisywanego przez większą niż 1 liczbę cech zdatności uwzględnia wspomniane zależności stochastyczne, wówczas analityczne metody wyznaczania wskaźników niezawodności (na podstawie znajomości tego modelu) zwykle zawodzą. W pewnych szczególnych przypadkach zastosowanie metody analitycznej jest jednak możliwe. Możliwość tę wskazuje podany związek między funkcją niezawodności obiektu złożonego o strukturze szeregowej a funkcjami niezawodności poszczególnych PK, wyprowadzone w ramach teorii korelacji przy założeniach: zmienne losowe Ti mają rozkłady normalne lub quasi-normalne (korelacja liniowa), a odpowiednie współczynniki korelacji rmh są nieujemne. Wykorzystując ten związek, można przedstawić wyrażenia na funkcję niezawodności obiektu złożonego przy uwzględnieniu zależności stochastycznych, podobne do formuł (44) i (45). Na przykład
gdzie
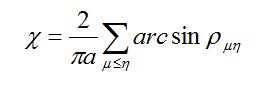
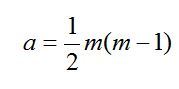 (47)
(47)
m, h = 1, 2,…, m
Rinf(t) – jest funkcją niezawodności PK najbardziej zawodnego.
Formuła (46) może być również wykorzystywana do wyznaczania funkcji niezawodności PK o n cechach zdatności, gdy n > 1. Wówczas
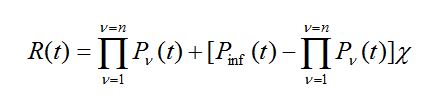 (48)
(48)
gdzie znaczenie symboli c i Pinf(t) podają relacje podobne do relacji (47).
Ponieważ wielkości występujące w wyrażeniu (46) i w wyrażeniu (48) zależą od różnych czynników konstrukcyjnych, technologicznych i eksploatacyjnych (p. np. zależności (43) i (44)), więc wyrażenia te stanowią poszukiwane szczegółowe postacie relacji (1) dla obiektu złożonego i dla pojedynczego PK.
Przy tej metodzie analitycznego wyznaczania niezawodności obiektu złożonego, model struktury niezawodnościowej powinien zawierać związki (33), na przykład w postaci (34), opisujące odpowiednie zależności stochastyczne. Wartości występujących tam współczynników korelacji rmh można wyznaczyć analitycznie lub za pomocą symulacji realizacji zmiennych losowych Tm i Th.
W wielu przypadkach założenia tej metody analitycznej (mówiące o normalności rozkładów cech zdatności Zn lub czasów Ti. oraz o nieujemnych wartościach współczynników korelacji rmh ) są jednak zbyt silne (choć w mniejszym stopniu w przypadku pojedynczego PK o wielu cechach zdatności), aby mogła być ona zastosowania do wyznaczania wskaźników niezawodności. Czasami wadę tę można częściowo wyeliminować przez odpowiedni dobór cech zdatności, zwłaszcza taki, aby współczynniki korelacji miały wartości nieujemne. Jednak komplikuje to wyznaczanie tych współczynników. Drugą wadą tej metody jest konieczność wyznaczania współczynników korelacji, co jest często kłopotliwe i żmudne, zwłaszcza przy sposobie analitycznym.
Podana w tej metodzie zależność (46) (lub zależność48) służy do wyznaczania funkcji niezawodności R(t). Również w zależnościach (44) i (45). służących do określenia poziomu niezawodności obiektu, używa się tylko tego wskaźnika
niezawodności. Znajomość tej funkcji może być jednak wykorzystana do wyznaczenia również i innych wskaźników. Tak na przykład intensywność niesprawności l(t) jest równa
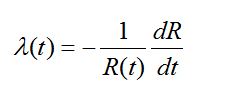 (49)
(49)
Sposoby wyznaczania innych wskaźników niezawodności na podstawie znajomości R(t), m.in. wartości oczekiwanej ET czasu bezawaryjnej pracy obiektu, podaje odpowiednia literatura z zakresu teorii niezawodności, np. prace [5, 24]. Wszystkie te wskaźniki dotyczą obiektów nieodnawianyoh (np. wielu elementów obiektów mechanicznych, a czasom nawet zespołów) oraz obiektów odnawianych w okresach między kolejnymi niesprawnościami. Wskaźniki te i przedstawione metody ich wyznaczania odnoszą się do procesu użytkowania obiektu. Za wskaźniki niezawodności obiektów odnawianych uznawane są również takie wielkości, jak współczynnik gotowości, wartość oczekiwana czasów odnów poawaryjnych i inne. Charakteryzują one jednak nie tyle obiekt, ile system obiekt-obsługa. Do wyznaczenia takich wskaźników konieczne jest zbudowanie nie tylko modelu użytkowania, lecz także odpowiedniego modelu obsługiwania obiektu (w ramach modelu eksploatacji obiektu). O trudnościach związanych z tym pisano już w podrozdz. 4.3, punkt b.
Powyżej przedstawiono kilka wybranych analitycznych metod badań niezawodności obiektu. Mogą być one stosowane do badań niezawodności PK i obiektu złożonego z wielu PK. Jeśli jednak nie można zrobić założenia o braku stochastycznych zależności między zmiennymi Ti lub założeń, przy których słuszna jest metoda wykorzystująca relację (46), to najwygodniejszą, a zwykle i jedyną, metodą badań niezawodności obiektu złożonego z wielu PK (lub opisanego wieloma cechami zdatności) jest metoda symulacji.